余弦定理の証明(鈍角に対向する辺の場合)

概要

任意のにおいて、角に対向する辺の長さをを用いて表し、以下に表される余弦定理を証明する。

\begin{eqnarray}
c^2=a^2+b^2-2ab \cos C
\end{eqnarray}

導出

が鋭角の場合を前回やったので、今回は図のように、鈍角の場合を考える。 

点から辺に垂線を引き、補助線としたいが、鋭角の時と異なり辺とは交わらない。そこで下図のように辺を延長し、補助線同士の交点をとする。

と辺を用いて、上図のようにとがわかる。また、なのでと表せる。

とのが邪魔なので消去したい。下に角度との関係を図示する。

これらの図を比較することで、、であることが分かる。

はを斜辺とする直角三角形であるので、三平方の定理より以下の関係が成り立つ。

\begin{eqnarray}
c^2&=&[b \sin (\pi-C)]^2 +[a+b\cos (\pi-C)]^2\\
\end{eqnarray}

を除去し、右辺を整理する。

\begin{eqnarray}
c^2&=&(b \sin C)^2 +(a-b\cos C)^2\\
&=& b^2 \sin^2 C+a^2-2ab \cos C +b^2 \cos ^2 C\\
&=&a^2+b^2(\sin ^2 C+ \cos ^2 C)-2ab \cos C\\
&=&a^2+b^2-2ab \cos C\\
\end{eqnarray}

が鈍角の場合にも余弦定理が導かれた。

また、が垂直の時、余弦定理は三平方の定理と等しいので証明済みである。そのため、任意ので余弦定理が成り立つことが導かれた。

余弦定理の証明(鋭角に対向する辺の場合)

概要

任意のにおいて、角に対向する辺の長さをを用いて表し、以下に表される余弦定理を証明する。

\begin{eqnarray}
c^2=a^2+b^2-2ab \cos C
\end{eqnarray}

導出

今回は図のように、が鋭角の場合を考える。

点から辺に垂線を引き、補助線とする。交点をとする。

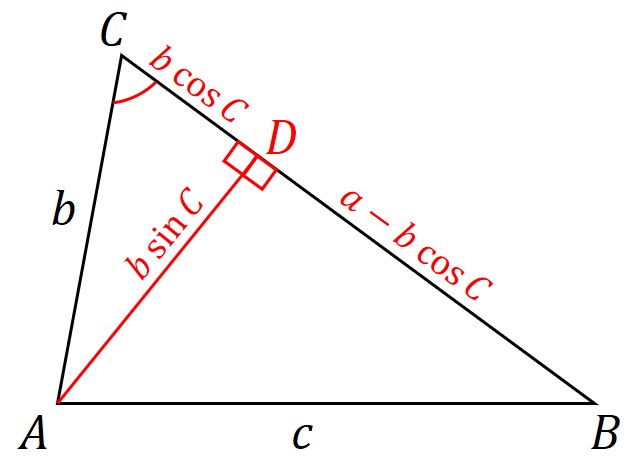
と辺を用いて、上図のようにとがわかる。また、なのでと表せる。

はを斜辺とする直角三角形であるので、三平方の定理より以下の関係が成り立つ。

\begin{eqnarray}
c^2&=&(b \sin C)^2 +(a-b\cos C)^2\\
&=& b^2 \sin^2 C+a^2-2ab \cos C +b^2 \cos ^2 C\\
&=&a^2+b^2(\sin ^2 C+ \cos ^2 C)-2ab \cos C\\
&=&a^2+b^2-2ab \cos C\\
\end{eqnarray}

を用いて、余弦定理が導かれた。

xが0に近い時のsin xの性質、面積を用いる方法

概要

図のように、半径の円(緑)と、二つの直角三角形(青、赤)を考える。これらの直角三角形と、切り取られる扇形の面積を比較して、三角関数の微分に必要なを導出する。

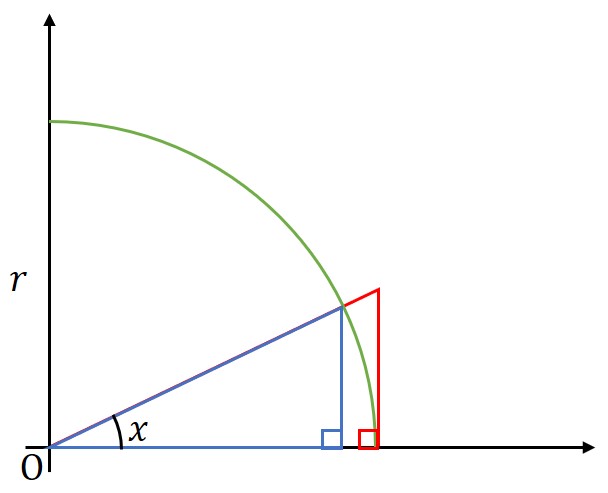
導出

まず二つの直角三角形と切り取られる扇形の面積を、円の半径と中心角を用いて表す。

小さな直角三角形の面積

斜辺がと定まることから底辺と高さを導ける。

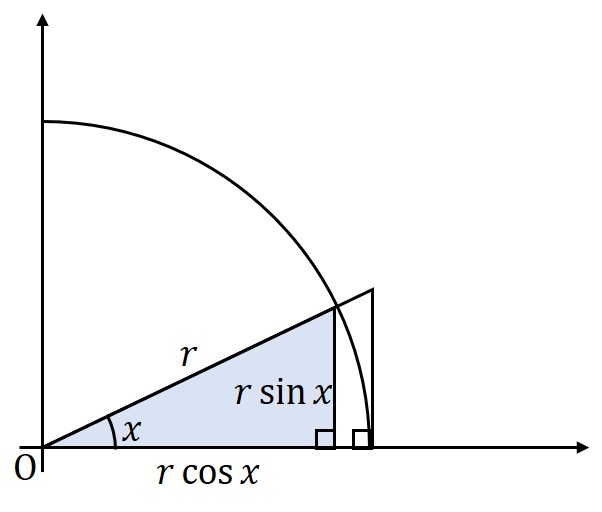
\begin{eqnarray}
S_1&=&\frac{1}{2}\times r \cos x \times r \sin x\\
&=&\frac{r^2 \sin x \cos x}{2}
\end{eqnarray}

切り取られる扇形の面積

円全体の面積に角度の割合をかけて求める。

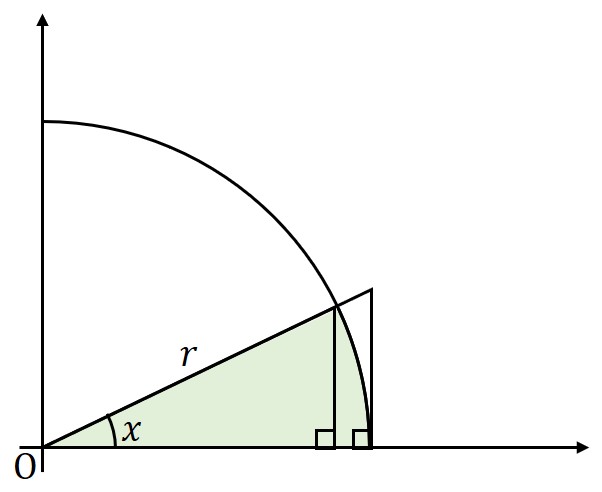
\begin{eqnarray}
S_2&=& \pi r^2 \times \frac{x}{2 \pi}\\
&=&\frac{r^2 x}{2}
\end{eqnarray}

大きな直角三角形の面積

底辺がと定まることから斜辺、高さの順に導ける。

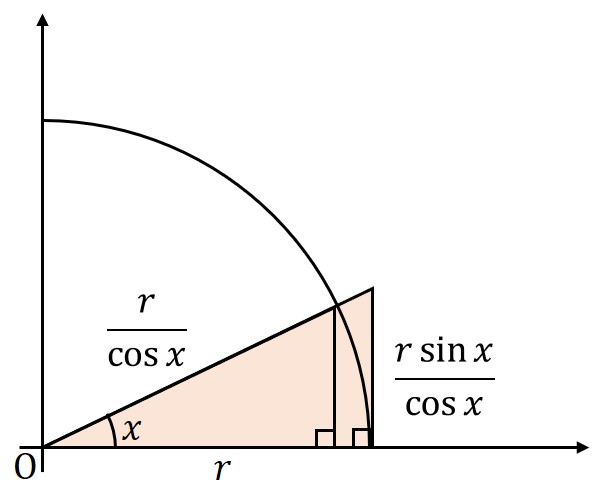
\begin{eqnarray}
S_3&=&\frac{1}{2} \times r \times \frac{r \sin x}{\cos x}\\
&=&\frac{r^2 \sin x}{2\cos x}
\end{eqnarray}

図を比較すると明らかに以下の関係が成り立つ。

\begin{eqnarray}
S_1<S_2<S_3
\end{eqnarray}

に計算した値を代入する。

\begin{eqnarray}
\frac{r^2 \sin x \cos x}{2}<\frac{r^2 x}{2}<\frac{r^2 \sin x}{2\cos x}
\end{eqnarray}

共通部分を打ち消す。
\begin{eqnarray} \require{cancel}
\frac{\cancel{r^2} \sin x \cos x}{\cancel{2}}&<&\frac{\cancel{r^2} x}{\cancel{2}}&<&\frac{\cancel{r^2} \sin x }{\cancel{2}\cos x}\\
\sin x \cos x&<&x&<&\frac{\sin x }{\cos x}
\end{eqnarray}

全体をで割る。としているので不等号の向きは変わらない。
\begin{eqnarray}
\cos x&<&\frac{x}{\sin x}&<&\frac{1}{\cos x}
\end{eqnarray}

全体の逆数を取る。不等号の向きが逆になる。
\begin{eqnarray}
\frac{1}{\cos x}&>&\frac{\sin x}{x}&>&\cos x
\end{eqnarray}

全体のを取る。

\begin{eqnarray}
\lim_{x \to 0}\frac{1}{\cos x}&>&\lim_{x \to 0}\frac{\sin x}{x}&>&\lim_{x \to 0}\cos x\\
1&>&\lim_{x \to 0}\frac{\sin x}{x}&>&1
\end{eqnarray}

はさみうちの原理により、以下の関係が求められた。

\begin{eqnarray}
\lim_{x \to 0}\frac{\sin x}{x}=1
\end{eqnarray}

またの時も、横軸の下側に2つの直角三角形と扇形を考えることができるので、この関係は同様に成り立つ。

xが0に近い時のsin xの性質 マクローリン展開を用いる方法

導出

以前導出したのマクローリン展開を書き下す。このマクローリン展開は無限の収束半径を持ち、本質的にと等しいのであった。

\begin{eqnarray} \sin x = x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots \end{eqnarray}

として両辺をで割る。

\begin{eqnarray} \frac{\sin x}{x} = 1-\frac{1}{3!}x^2+\frac{1}{5!}x^4-\frac{1}{7!}x^6+\cdots \end{eqnarray}

両辺のを取る。

\begin{eqnarray} \require{cancel} \lim_{x \to 0}\frac{\sin x}{x} &=& \lim_{x \to 0} \left( 1-\frac{1}{3!}x^2+\frac{1}{5!}x^4-\frac{1}{7!}x^6+\cdots \right) \newline &=&\lim_{x \to 0} \left( 1-\cancel{\frac{1}{3!}x^2}+\cancel{\frac{1}{5!}x^4}-\cancel{\frac{1}{7!}x^6}+\cancel{\cdots} \right) \newline &=&1 \end{eqnarray}

すなわち、がにとても近い時、はに収束する。

しかし、ちょうどの時は、分母と分子が両方ともになってしまっての値が定まらず、成り立たないことに注意。

この計算に意味あるの？

この計算は、三角関数の微分に必要な知識を導出するためのものである。

しかしよく考えるとをマクローリン展開する時点ですでに三角関数の微分を使用してしまっているので、循環論法になってしまって意味がない。

そのため多くの場合、扇形の面積や弧の長さを用いた幾何的な手法でを導出する。

しかしながら、幾何的な導出こそが循環論法であるとする流派もある。(円の面積をちゃんと計算するために積分が必要だから、そこでを使わないといけないよ派）

その流派では、は図形と無関係にマクローリン展開形式で定義されることになる。（これは導出ではなく定義なので、三角関数の微分は必要ないという理屈） \begin{eqnarray} \sin x = x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots \end{eqnarray}

この場合、最初にを知ることができるのは今回の手法になるのである。

参考 https://sci-tech.ksc.kwansei.ac.jp/~kawanaka/sinx.pdf

民主主義は三択に弱い

背景

最近ブレグジット問題がアツい。イギリスがEU離脱を決定したものの、その離脱プロセスが決まらず、締め切りだけが迫っている状況なのだ。

締め切りが来ると何も決まってないのに強制的にEU離脱となって大混乱を招くという。一体何故こんなことになってしまったのだろうか。

以下、モデル化してブレグジット投票の流れを追う。

イギリスの有権者3パターン

大体以下の3パターンに分かれている。

• EU残留派 40%「EUに残留したい、離脱絶対反対！」
• ソフト離脱派30%「EUからは離脱したいけど、ちゃんと交渉に沿ってやる」
• ハード離脱派30%「EUから離脱したい！交渉で妥協とかしない！」

支持率の数値は適当なので注意。モデル化上、重要な所は以下の2点にある。

• どの派閥も単独では過半数を取れない
• 離脱派を合計すると過半数を超える

また国民投票と議員による投票があるのだが区別していない。

投票

1回目

「イギリスはEUから離脱することにしますか？」

• EU残留派 40%「No！」
• ソフト離脱派30%「Yes！」
• ハード離脱派30%「Yes！」

離脱賛成60%で過半数。離脱が決定した。次は具体的な方針を決めよう。

2回目

「EUと妥協点を探って離脱する計画を作りました。でもEUの影響は残るかも…これで良い？」

• EU残留派 40%「離脱したくないからNo！」
• ソフト離脱派30%「Yes！」
• ハード離脱派30%「手緩いからNo！」

反対70%で過半数。ソフトブレグジットしないことが決定した。

3回目

「じゃあ問答無用で離脱することにする？」

• EU残留派 40%「離脱しないって言ってるだろ！No！」
• ソフト離脱派30%「無茶苦茶すぎるだろ！No！」
• ハード離脱派30%「Yes！」

反対70%で過半数。ハードブレグジットしないことが決定した。

4回目

「分かった。ホントは離脱したくなかったんだろ？国民投票をもう一度やろう？」

• EU残留派 40%「それだ！Yes！」
• ソフト離脱派30%「No！」
• ハード離脱派30%「No！」

反対60%で過半数。再投票しないことが決定した。

なぜこんなことに…

つまり3択で、自分の意見とぴったりでないとNo投票する、というルールで投票を行うと、全て否決されてしまって永遠に何の結論も出なくなってしまう。

また、今回は3パターンの別れかたが、「強賛成」「弱賛成」「反対」だったことが問題を危険にしている。「賛成派」自体は過半数を超えているので、取り消すこともできずに時間だけが過ぎてしまったのだ。

日本の場合

例えば大阪都構想はこれと近い動きをしているが、層の別れ方が異なったのでセーフだった。

• 「維新の会も大阪都構想も好き」30%
• 「維新の会は好きだけど都構想は嫌」30%
• 「維新の会も都構想も嫌」40%

の三層がいるので、

維新の会が選挙で勝つ！

↓

大阪都構想や！

↓

アカン！票が足らん！これは解散しかない…

↓

解散後の選挙でまた維新の会が勝つ！

↓

これは大阪都構想待ったなしや！

の繰り返しが発生してしまう。維新の会は普通に人気があるので、都構想投票に失敗した後も選挙で勝ってしまうのだった。

しかしこれは都構想賛成派が過半数いないため、つまり「賛成」「弱反対」「強反対」に分かれたため、グルグル回るだけでイギリスみたいな決定的な問題にはならなかった。

最後はどうするのか？

メイ首相(ソフト離脱派)は「相手の思うツボですよ作戦」を取っていくのではないか？

残留派には「時間切れになったら結局ハードブレグジットになっちゃいますよ？」

ハード離脱派には「このままモタモタしてたら離脱延期しかないですよ。その間に流れが変わって再投票になったりするかも？」

と脅しをかけて、ソフト離脱派プランに同意するようプッシュするという作戦なのでは。

これがうまく行くかはもう政治家の力量と妥協の世界なのでどうなるのかは俺程度では分からないのだった。（ゲーム理論とかにあるのかも知れないけど）

指数表記された三角関数の手触りを確かめる

前回までに、オイラーの公式を用いて三角関数を指数関数形式で表せることを示した。

この形式でも三角関数としての性質が保たれていることを、いくつかの代表的な性質から確認する。

との指数関数表記を再度書く。

\begin{eqnarray}
\sin x&=&\frac{e^{ix}-e^{-ix}}{2i}
\end{eqnarray}

\begin{eqnarray}
\cos x&=&\frac{e^{ix}+e^{-ix}}{2}
\end{eqnarray}

を確かめる。

左辺を変形して右辺を目指す。

\begin{eqnarray}
\sin 0&=&\frac{e^{i0}-e^{-i0}}{2i}\\&=&\frac{1-1}{2i}\\&=&0
\end{eqnarray}

合っている。

を確かめる。

左辺を変形して右辺を目指す。

\begin{eqnarray}
\cos 0&=&\frac{e^{i0}+e^{-i0}}{2}\\&=&\frac{1+1}{2}\\&=&1
\end{eqnarray}

合っている。

を確かめる。

左辺を変形して右辺を目指す。

\begin{eqnarray} \require{cancel}
\sin^2 x+ \cos^2 x&=&\left(\frac{e^{ix}-e^{-ix}}{2i}\right)^2+\left(\frac{e^{ix}+e^{-ix}}{2}\right)^2\\
&=&\frac{e^{2ix}-2+e^{-2ix}}{-4}+\frac{e^{2ix}+2+e^{-2ix}}{4}\\
&=&\frac{\cancel{-e^{2ix}}+2-\xcancel{e^{-2ix}}}{4}+\frac{\cancel{e^{2ix}}+2+\xcancel{e^{-2ix}}}{4}\\
&=&1
\end{eqnarray}

合っている。

を確かめる。

左辺を変形して右辺を目指す。

\begin{eqnarray} \require{cancel}
( \sin x)'&=&\left( \frac{e^{ix}-e^{-ix}}{2i} \right)'\\
&=&\frac{i e^{ix}+i e^{-ix}}{2i}\\
&=&\frac{\cancel{i}e^{ix}+\cancel{i}e^{-ix}}{2\cancel{i}}\\
&=&\frac{e^{ix}+e^{-ix}}{2}\\
&=& \cos x
\end{eqnarray}

合っている。

を確かめる。

左辺を変形して右辺を目指す。

\begin{eqnarray}
( \cos x)'&=&\left( \frac{e^{ix}+e^{-ix}}{2} \right)'\\
&=&\frac{i e^{ix}-i e^{-ix}}{2}
\end{eqnarray}

分子と分母にをかける。

\begin{eqnarray}
(\cos x)'&=&\frac{-e^{ix}+e^{-ix}}{2i}\\
&=&-\frac{e^{ix}-e^{-ix}}{2i}\\
&=& -\sin x
\end{eqnarray}

合っている。

を確かめる。

今回は右辺を変形して左辺を目指す。

\begin{eqnarray} \require{cancel}
2 \sin x \cos x&=&2 \cdot \frac{e^{ix}-e^{-ix}}{2i} \cdot \frac{e^{ix}+e^{-ix}}{2}\\
&=&2 \cdot \frac{e^{2ix}-e^{2ix}}{4i}\\
&=&\frac{e^{2ix}-e^{2ix}}{2i}\\
&=&\sin 2x
\end{eqnarray}

合っている。

を確かめる。

今回は右辺を変形して左辺を目指す。

\begin{eqnarray} \require{cancel}
\sin a\cos b+\cos a \sin b &=&\frac{e^{ia}-e^{-ia}}{2i} \cdot \frac{e^{ib}+e^{-ib}}{2}+\frac{e^{ia}+e^{-ia}}{2} \cdot \frac{e^{ib}-e^{-ib}}{2i}\\
&=&\frac{e^{i(a+b)}-\cancel{e^{i(b-a)}}+\xcancel{e^{i(a-b)}}-e^{-i(a+b)}}{4i}+\frac{e^{i(a+b)}-\xcancel{e^{i(a-b)}}+\cancel{e^{i(b-a)}}-e^{-i(a+b)}}{4i}\\
&=&\frac{2e^{i(a+b)}-2e^{-i(a+b)}}{4i}\\
&=&\frac{e^{i(a+b)}-e^{-i(a+b)}}{2i}\\
&=&\sin (a+b)
\end{eqnarray}

合っている。

代表的な三角関数の性質が、指数関数表記でも成り立っていることが確かめられた。

オイラーの公式から導かれる三角関数の記法

概要

オイラーの公式を受け入れると三角関数を別の形式で表せる。

導出

オイラーの公式を再度書く。

\begin{eqnarray}
e^{ix}=\cos x+i\sin x
\end{eqnarray}

式中のをに置き換えてみる。 

\begin{eqnarray}
e^{-ix}&=&\cos (-x)+i\sin (-x)\\
&=&\cos x-i\sin x
\end{eqnarray}

は偶関数なので変化しない。は奇関数なのでマイナスが付く。

マクローリン展開版の表記でも確認しておく。まず元の形。

\begin{eqnarray}
e^{ix}&=&\left(1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\cdots\right)+i\left(x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\cdots\right)\\
\end{eqnarray}

式中のをに置き換えてみる。

\begin{eqnarray}
e^{-ix}&=&\left(1-\frac{1}{2!}(-x)^2+\frac{1}{4!}(-x)^4-\cdots\right)+i\left((-x)-\frac{1}{3!}(-x)^3+\frac{1}{5!}(-x)^5-\cdots\right)\\
&=&\left(1-\frac{1}{2!}x^2+\frac{1}{4!}x^4-\cdots\right)-i\left(x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\cdots\right)
\end{eqnarray}

実部にはが偶数次の項しかないので変化しない。虚部には奇数次の項しかないので結局虚部全体にマイナスが付き、同じ結果が得られた。

この結果を踏まえてを計算する。

\begin{eqnarray} \require{cancel}
e^{ix}+e^{-ix}&=&(\cos x+ i \sin x)+(\cos x-i\sin x)\\
&=&\cos x+ \cancel{i \sin x} + \cos x-\cancel{i\sin x}\\
&=& 2 \cos x
\end{eqnarray} 

について式変形する。

\begin{eqnarray}
2 \cos x&=&e^{ix}+e^{-ix}\\
\cos x&=&\frac{e^{ix}+e^{-ix}}{2}
\end{eqnarray}

の新たな記法が導かれた。

同様にを計算する。

\begin{eqnarray} \require{cancel}
e^{ix}-e^{-ix}&=&(\cos x+ i \sin x)-(\cos x-i\sin x)\\
&=&\cancel{\cos x}+ i \sin x -  \cancel{\cos x}+i\sin x\\
&=& 2i \sin x
\end{eqnarray} 

について式変形する。

\begin{eqnarray}
2i \sin x&=&e^{ix}-e^{-ix}\\
\sin x&=&\frac{e^{ix}-e^{-ix}}{2i}
\end{eqnarray}

の新たな記法が導かれた。