2020-03-07

半減期を微分方程式で表すその2

概要

前回、放射性物質の個数を表す微分方程式を導いた。微分方程式を解いて放射性物質が減っていく様子を式で表す。

式

解きたい微分方程式をもう一度書く。

\begin{eqnarray}
\frac{dN(t)}{dt}=-\lambda N(t)
\end{eqnarray}

変数分離法で解く。 $N(t) \neq 0$ として、両辺を $N(t)$ で割る。

\begin{eqnarray}
\frac{1}{N(t)}\frac{dN(t)}{dt}=-\lambda
\end{eqnarray}

両辺を $t$ で積分する。

\begin{eqnarray} \require{cancel}
\int \frac{1}{N(t)}\frac{dN(t)}{dt} dt&=& \int -\lambda dt \\
\int \frac{1}{N(t)}\frac{dN(t)}{\cancel{dt}} \cancel{dt}&=& \int -\lambda dt
\end{eqnarray}

積分を実行する。 $C$ は任意定数である。

\begin{eqnarray}
\ln |N(t)|=-\lambda t + C
\end{eqnarray}

指数関数として書き直す。

\begin{eqnarray}
|N(t)|&=&e^{-\lambda t +C}\\
N(t)&=&\pm e^{-\lambda t +C}\\
N(t)&=&\pm e^Ce^{-\lambda t}\\
N(t)&=&Ce^{-\lambda t}
\end{eqnarray}

$\pm e^C$ を改めて $C$ と置きなおした。

$t=0$ を考えてみる。

\begin{eqnarray}
N(0)&=&C e^{-\lambda 0}\\
N(0)&=&C
\end{eqnarray}

すなわち、積分定数 $C$ は放射性物質の初期個数を表すので、 $C=N_0$ と書くことにする。

\begin{eqnarray}
N(t)=N_0 e^{-\lambda t}
\end{eqnarray}

一般解が導かれた。

より半減期が分かりやすいように指数関数の底を $e$ から $2$ に変換して書き直す。式変形のため、以下のように置いておく。

\begin{eqnarray}
e^{- \lambda t}=y
\end{eqnarray}

両辺の $\log_2$ を取る。

\begin{eqnarray}
\log_2 e^{- \lambda t}=\log_2 y\\
- \lambda t \log_2 e=\log_2 y
\end{eqnarray}

$y$ について整理する。

\begin{eqnarray}
y=2^{- \lambda t \log_2 e}
\end{eqnarray}

$y=e^{- \lambda t }$ を代入する。

\begin{eqnarray}
e^{-\lambda t}=2^{- \lambda t \log_2 e}
\end{eqnarray}

指数関数の基数を $e$ から $2$ に変換できた。

$\log_2 e=1.44...$ であるので、これを代入する。

\begin{eqnarray}
N(t)&=&N_0 e^{-\lambda t}\\
&=&N_0 2^{-1.44\lambda t}
\end{eqnarray}

放射性物質の個数 $N(t)$ を表す式が求められた。

$N(t)$ が $N(0)$ の半分になる時間 $t_\rm{h}$ は、 $2$ にかかる指数 $-1.44 \lambda t_\rm{h}$ が $-1$ になる時なので、

\begin{eqnarray}
-1.44 \lambda t_\rm{h} &=& -1\\
t_\rm{h}&=&\frac{1}{1.44 \lambda}
\end{eqnarray}

が半減期を表す。 $\lambda$ は崩壊しやすさを表す正の比例定数であった。それが大きいほど半減期 $t_\rm{h}$ が短くなることが式に表れている。

さらに $t_\rm{h}=\frac{1}{1.44 \lambda}$ を代入すれば、次のように短く書ける。

\begin{eqnarray}
N(t)&=&N_0 2^{-1.44\lambda t}\\
&=&N_0 2^{-\frac{t}{t_\rm{h}}}
\end{eqnarray}

$2$ にかかる指数は、経過時間 $t$ と半減期 $t_\rm{h}$ の比率になっているので、これらの単位が同じなら計算可能である。SI単位系の時間は「秒」だが、両方とも「年」としてもよいのである。これは崩壊の比例定数 $\lambda$ の時間単位を任意にとって良いことに対応している。

2020-02-29

半減期を微分方程式で表すその1

概要

放射性原子が崩壊して残りの個数が減っていく様子を微分方程式から導き、半減期の概念を理解する。今回は解きたい微分方程式を作るところまで説明する。

考え方

放射性原子は全ての時刻でランダムに一定確率で崩壊する、この「一定確率で減っていく」ことをどのように扱うか、というのが難しいのだが、以下のように言い換えることで式に表すことができる。

「ランダムに一定確率で崩壊する」ということはすなわち、以下の2つの文章に等しい。

「崩壊する原子の数は元の原子の数に比例する」
= 元の原子の数が2倍になったら崩壊する数も2倍になる

「崩壊する原子の数は観察する期間に比例する」
= 観察する期間が2倍になったら崩壊する数も2倍になる

立式

両辺を原子の数の変化として微分方程式を作る。時刻 $t$ における放射性物質の残数を $N(t)$ で表す。

\begin{eqnarray}
N(t+\Delta t)-N(t)=-\lambda N(t) \Delta t
\end{eqnarray}

ここで $\Delta t$ が上述した観察期間に相当する。比例定数 $\lambda$ 自体は正の値として、マイナスをつけることで原子の減少を表す。

$\Delta t \neq 0$ として両辺を $\Delta t$ で割る。

\begin{eqnarray}
\frac{N(t+\Delta t)-N(t)}{\Delta t}=-\lambda N(t)
\end{eqnarray}

両辺の $\displaystyle \lim_{\Delta t \to 0}$ を取る。

\begin{eqnarray}
\lim_{\Delta t \to 0} \frac{N(t+\Delta t)-N(t)}{\Delta t}=\lim_{\Delta t \to 0} -\lambda N(t)
\end{eqnarray}

左辺が微分の定義に等しいことを用いて書き換える。右辺には $\Delta t$ がないので $\displaystyle \lim_{\Delta t \to 0}$ を取っても変わらない。

\begin{eqnarray}
\frac{dN(t)}{dt}=-\lambda N(t)
\end{eqnarray}

求めたい微分方程式が導かれた。

2020-02-23

C14年代測定を式で表す

概要

土中から発掘された遺跡や化石が何年前のものなのか分析するための手法、 $\rm C14$ 年代測定を式で示す。

原理

炭素の放射性同位体 $\rm C14$ は宇宙線により毎年生産され、同時にβ崩壊により毎年消滅している。これらの平衡により地球上の炭素原子に占める $\rm C14$ の割合は $\displaystyle \frac{1}{10^{12}}$ に保たれている。

また、生物は常に環境からの炭素摂取と排出を繰り返しているため、体内の $\rm C14$ もまた同じ割合に保たれている。しかし生物が死亡すると炭素の摂取が止まるため、遺骸内の $\rm C14$ 量は減少していく。

これを用いて生物がいつ死亡したかを判定するのが $\rm C14$ 年代測定である。どのように年代を分析するかを式で表す。

$\rm C14$ の半減期は5730年であり、5730年経過するごとに遺骸内の $\rm C14$ は元の量の半分になる。これは以下のような式で表せる。

\begin{eqnarray}
x \times \left( \frac{1}{2} \right) ^\frac{y}{5730} = z
\end{eqnarray}

ここで $x$ は当初の $\rm C14$ の割合、 $y$ が経過した年数、 $z$ が経過後の $\rm C14$ の割合である。

$x$ に死んだ直後における $\rm C14$ の割合 $\displaystyle \frac{1}{10^{12}}$ 、 $z$ に現在の(測定された) $\rm C14$ の割合を代入して $y$ を求めることができる。

$y$ について式変形していく。

\begin{eqnarray}
\left( \frac{1}{2} \right) ^\frac{y}{5730} &=& \frac{z}{x}\\
2 ^{\frac{-y}{5730}} &=& \frac{z}{x}\\
\end{eqnarray}

両辺の $\log_2$ を取る。

\begin{eqnarray}
{\frac{-y}{5730}} &=& \log_2 {\frac{z}{x}}\\
y&=&-5730 \log_2 {\frac{z}{x}}
\end{eqnarray}

$x = \frac{1}{10^{12}}$ を代入する。

\begin{eqnarray}
y&=&-5730 \log_2 {(10^{12}z)}
\end{eqnarray}

経過年数 $y$ を求める式が導かれた。変数は測定値 $z$ だけなので、 $\rm C14$ の割合を測定するだけで年代測定ができることがわかる。

この手法は化石などの生物遺骸には有効だが、土器などの非生物は測定出来ない。同時に出土した木材や食材を用いて間接的に測定する必要がある。

2020-02-15

バーゼル問題

概要

$s$ 次ゼータ関数 $\displaystyle \zeta(s)=\sum_{k=1}^{\infty}\frac{1}{k^s}$ の収束判定を行いたい。これまでに $\zeta(1)$ は無限大に発散し、 $\zeta(2)$ は2よりも小さい数に収束することを示してきた。

$\zeta(2)$ が実際いくつに収束するのかを求める。以下に $\zeta(2)$ を書き下しておく。

\begin{eqnarray} \zeta(2)&=&\sum_{k=1}^{\infty}\frac{1}{k^2}\ &=&\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots \end{eqnarray}

導出

$\sin x$ のマクローリン展開を書き下す。

\begin{eqnarray} \sin x&=&x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots\ \end{eqnarray}

$x \neq 0$ として、両辺を $x$ で割る。

\begin{eqnarray} \frac{\sin x}{x}&=&1-\frac{1}{3!}x^2+\frac{1}{5!}x^4-\frac{1}{7!}x^6+\cdots \end{eqnarray}

右辺の無限べき関数を因数分解したい。どうすれば良いだろうか？

べき関数 $\displaystyle y = \sum_{n=0}^{\infty} {a_n} x^n$ が $x$ 軸と交差する点、 $\pm \pi, \pm 2\pi, \pm 3\pi, \cdots$ を用いて、右辺を因数分解できる。

\begin{eqnarray} \frac{\sin x}{x}&=&\left( 1-\frac{x}{\pi} \right) \left( 1+\frac{x}{\pi}\right) \left( 1-\frac{x}{2\pi}\right) \left( 1+\frac{x}{2\pi}\right)\left( 1-\frac{x}{3\pi}\right) \left( 1+\frac{x}{3\pi}\right)\cdots \end{eqnarray}

※ この時、右辺を定数倍したものも解を満たすが、 $\displaystyle \lim_{x \to 0} \frac{\sin {x}}{x}=1$ を用いて本式に定まる。

$(a+b)(a-b)=a^2-b^2$ を用いて右辺を変形する。 \begin{eqnarray} \frac{\sin x}{x}&=&\left( 1-\frac{x^2}{\pi^2}\right)\left( 1-\frac{x^2}{2^2\pi^2}\right)\left( 1-\frac{x^2}{3^2\pi^2}\right)\cdots\\ &=&1- \left( \frac{1}{\pi^2}+\frac{1}{2^2\pi^2} + \frac{1}{3^2\pi^2} \cdots \right) x^2 + \cdots \end{eqnarray} 展開して昇べきの順にまとめた。

マクローリン展開形式と昇べき形式の $x^2$ の項を比較する。これらは等しいはずなので以下が成り立つ。 \begin{eqnarray} \frac{1}{3!} &=& \frac{1}{\pi^2}+\frac{1}{2^2\pi^2} + \frac{1}{3^2\pi^2}+\cdots \\ \frac{1}{6} &=& \frac{1}{\pi^2} \left( \frac{1}{1^2}+\frac{1}{2^2} + \frac{1}{3^2} + \cdots \right)\\ \frac{\pi^2}{6} &=& \frac{1}{1^2}+\frac{1}{2^2} + \frac{1}{3^2} + \cdots \\ \end{eqnarray}

ここで右辺は $\zeta(2)$ の定義そのものであるので、以下のように表せる。 \begin{eqnarray} \displaystyle \zeta(2)=\sum_{k=1}^{\infty}\frac{1}{k^2}=\frac{\pi^2}{6} \\ \end{eqnarray}

また、 $\displaystyle \frac{\pi^2}{6}=1.64 \cdots$ であるので、 $\zeta(2)$ は2よりも小さい数に収束することが確かめられた。

2020-01-12

マクスウェル方程式を導く準備

マクスウェル方程式とは

電磁気に関する実験的事実をスタートとして、論理的考察(電場と磁場)を加え、微分方程式で表したもの。

4つの実験的事実が4つの方程式で表される。マクスウェル方程式を解くことで、電磁波の存在や、光もまた電磁波であることなどの重要な事実が導かれる。

実験的事実

マクスウェル以前に実験で確かめられた4つの法則。

1. 電荷のクーロンの法則

電荷には+と-の2種類が存在する
電荷が同じ符号だと斥力、違う符号だと引力を持つ
引力と斥力はどちらも、電荷の量に比例し、距離の2乗に反比例する

2. 電磁誘導の法則

電線に磁石を近づけたり遠ざけたりすると電線の両端に電位差が発生する
発生する電位差は、磁石を動かす速度に比例する
発生する電位差の向きは、アンペールの法則で磁力の変動を妨げる方向になる

3. 磁荷のクーロンの法則

磁荷にはN(+)とS(-)の2種類が存在する
磁荷が同じ符号だと斥力、違う符号だと引力を持つ
引力と斥力はどちらも、磁荷の量に比例し、距離の2乗に反比例する
単磁極は存在せず、磁石は必ずN極とS局のペアで存在する

4. アンペールの法則

電線に電流を流すと、周囲に磁力が発生する
磁力の強さは、電流に比例し、電線からの距離に反比例する。
発生する磁力の向きは右ねじの法則にしたがう

論理的考察

実験的事実を解釈する際に想像されたもの。

電場

電荷に対して力を及ぼす空間のこと
電荷や電圧によって発生する

磁場

磁荷に対して力を及ぼす空間のこと
磁荷や電流によって発生する

電場と磁場の実在性

電場と磁場が「計算上便利だから導入された想像上の物なのか？それとも本当に存在するものなのか？」は電磁気学にとって重要な問題である。マクスウェル方程式を解くことにより、電場と磁場の実在が確かめられる。

マクスウェル方程式の二つの記法

マクスウェル方程式には「積分形」と「微分形」の2つの記法があり、「微分形」の方が有名。

積分形までは上記事実と論理的考察のみでたどり着くことができるが、微分形は積分形に対して純粋に数学的な書き換えを行わなければ得られない。

2019-08-18

一次元の熱方程式を導く

概要

十分細く、一次元とみなせる針金の温度分布と、その経時変化を考えたい。まず解くべき微分方程式を導出する。

針金上の座標を $x \: \rm{[m}]$ 、時間を $t \: \rm{[sec]}$ 、温度を $T(x,t) \: \rm{[K]}$ とする。

f:id:dai-ig:20190901110610j:plain:w480

また、熱の流れ $\Gamma (x,t) \: \rm{[J/sec]}$ を考える。

導出

熱の流れについての式

熱の流れ $\Gamma$ は温度の勾配 $\displaystyle \frac{\partial T}{ \partial x}$ に比例する。(フーリエの法則)

この関係は以下のように式で表せる。

\begin{equation} \Gamma (x,t)=-k\frac{\partial}{ \partial x} T(x,t) \tag{1} \end{equation}

ここで、温度 $T$ は $x$ と $t$ 両方の関数としたので、偏微分になる。

$k$ は熱流の通りやすさを示す、熱伝導率と呼ばれる正の比例定数であり、針金の材質で決まる。熱は温度が高い方から低い方に流れるので、温度勾配とは逆方向に流れる。そのため $k$ の前にマイナスがついている。

針金上の一次元区間 $(a, b )$ を考える。

f:id:dai-ig:20190901110810j:plain:w480

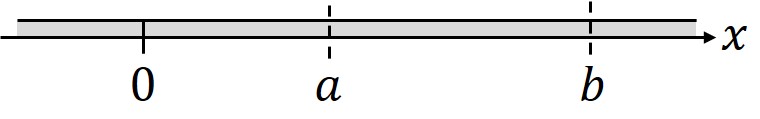
それぞれの点の熱流を式(1)形式で表す。

\begin{equation} \Gamma (a,t)=-k \left. \frac{\partial}{ \partial x} T(x,t)\right|_{x=a} \end{equation}

\begin{equation} \Gamma (b,t)=-k \left. \frac{\partial}{ \partial x} T(x,t)\right|_{x=b} \end{equation}

点 $a$ と点 $b$ を通した熱流の出入りの総和は以下のように書ける。

\begin{equation} \Gamma(b,t)-\Gamma(a,t)=\int^b_a \frac{\partial}{\partial x} \Gamma(x,t) dx \tag{2} \end{equation}

式(2)を確認するため、右辺の定積分を実際にやってみよう。

\begin{eqnarray} 右辺&=&\int^b_a \frac{\partial}{\partial x} \Gamma(x,t) dx \\ &=&\bigl[\Gamma(x,t) \bigr]^b_a \\ &=&\Gamma(b,t)-\Gamma(a,t) \\ &=& 左辺 \end{eqnarray}

等式が確認された。

式2に $\Gamma(a,t),\Gamma(b,t)$ および $\Gamma(x,T)$ の中身を代入する。

\begin{eqnarray} −k\frac{∂}{∂x}T(x,t)|_{x=a}+k\frac{∂}{∂x}T(x,t)|_{x=b}=−k\int^b_a\frac{∂^2}{∂x^2}Γ(x,t)dx \end{eqnarray}

熱量についての式

一方、区間 $(a,b)$ に蓄えられている熱量は以下のように書ける。

\begin{equation} Q(t)=c\int ^b_a T(x,t) dx \end{equation}

$c$ は物質の温まりにくさを示す正の比例定数であり、(単位長さ当たりの)熱容量と呼ばれる。値は針金の材質で決まる。

$Q(t)$ の時間変化を考える。両辺を $t$ で微分する。ここで、 $Q(t)$ は $t$ だけの関数なので全微分である。

\begin{eqnarray} \frac{d}{dt}Q(t)&=&c\frac{∂}{∂t}∫_a^b T(x,t) dx \\ &=& c∫_a^b \frac{∂}{∂t} T(x,t) dx \end{eqnarray}

微分と積分の順序を交換した。

二つの式を合体

熱量の保存則より以下の関係が成り立つ。

\begin{eqnarray} \frac{d}{dt} Q(t)=出入りする熱量の合計 \end{eqnarray}

左辺と右辺の中身はここまでに解っているので、それぞれ代入する。 \begin{eqnarray} c∫_a^b\frac{∂}{∂t} T(x,t) dx = k∫^b_a\frac{∂^2}{∂x^2} Γ(x,t) dx \end{eqnarray}

この関係が全ての $(a,b)$ で成り立つためには積分の対象が等しい必要がある。 \begin{eqnarray} c\frac{∂}{∂t}T(x,t)=k\frac{∂^2}{∂x^2}Γ(x,t) \end{eqnarray}

一次元の熱方程式が導かれた。この微分方程式を解くことで、針金の温度分布とその時間変化が求められる。

2019-05-28

円の面積の導出

幾何数学

概要

以前、弧の長さを用いて導出した等式、 $\displaystyle \lim_{x \to 0} \frac{\sin x}{x}=1$ を用いて、半径 $r$ を持つ円の面積を導出する。

導出

半径 $r$ の円に内接する正 $n$ 角形と円に外接する正 $n$ 角形を考える。 $n=6$ の場合を図に示す。

f:id:dai-ig:20200126145130p:plain:w480

下図のように、円と正 $n$ 角形をを $2n$ 等分して考える。

f:id:dai-ig:20200126145212p:plain:w480

まず二つの直角三角形と切り取られる扇形の面積を、円の半径 $r$ と中心角 $x$ を用いて表す。

小さな直角三角形の面積 $S_1$

斜辺が $r$ と定まることから底辺と高さを導ける。

f:id:dai-ig:20200126151223p:plain:w400

\begin{eqnarray} S_1&=&\frac{1}{2}\times r \cos x \times r \sin x\newline &=&\frac{r^2 \sin x \cos x}{2} \end{eqnarray}

切り取られる扇形の面積 $S_2$

未知の値。この値を求めてから $2n$ 倍すれば円の面積が求められる。

f:id:dai-ig:20200126151545p:plain:w360

大きな直角三角形の面積 $S_3$

底辺が $r$ と定まることから斜辺、高さの順に導ける。

f:id:dai-ig:20200126152030p:plain:w480

\begin{eqnarray} S_3&=&\frac{1}{2} \times r \times \frac{r \sin x}{\cos x}\ &=&\frac{r^2 \sin x}{2\cos x} \end{eqnarray}

面積の比較

図を重ねて比較すると明らかに以下の関係が成り立つ。

\begin{eqnarray} S_1<S_2<S_3 \end{eqnarray}

$S_1$ と $S_3$ に計算した値を代入する。

\begin{eqnarray} \frac{r^2 \sin x \cos x}{2}<S_2<\frac{r^2 \sin x}{2\cos x} \end{eqnarray}

$x > 0$ として全体を $x$ で割り、 $\displaystyle \frac{ \sin x }{ x }$ の形を作る。

\begin{eqnarray} \frac{ r^2 }{ 2 } \frac{ \sin x }{ x } \cos x&<&\frac{S_2}{x}&<&\frac{r^2}{2 }\frac{ 1 }{ \cos x }\frac{ \sin x}{ x } \end{eqnarray}

ここで、 $n$ 角形を、 $\infty$ 角形に近づけていく。この時中心角 $x$ は限りなく $0$ に近づく。

\begin{eqnarray} \lim_{x \to 0} \frac{ r^2 }{ 2 } \frac{ \sin x }{ x } \cos x&<& \lim_{x \to 0}\frac{S_2}{x}&<& \lim_{x \to 0}\frac{r^2}{2 }\frac{ 1 }{ \cos x }\frac{ \sin x}{ x } \end{eqnarray}

$\displaystyle \lim_{x \to 0}\frac{ \sin x }{x }=1$ を用いる。

\begin{eqnarray} \require{cancel} \lim_{x \to 0} \frac{ r^2 }{ 2 } \cancel {\frac{ \sin x }{ x } }\cos x&<& \lim_{x \to 0}\frac{S_2}{x}&<& \lim_{x \to 0}\frac{r^2}{2 }\frac{ 1 }{ \cos x }\cancel{\frac{ \sin x}{ x }} \newline \lim_{x \to 0}\frac{ r^2 }{ 2 }\cos x&<& \lim_{x \to 0}\frac{S_2}{x}&<& \lim_{x \to 0} \frac{ r^2 }{ 2 }\frac{1}{\cos x} \newline \frac{ r^2 }{ 2 }&<& \lim_{x \to 0}\frac{S_2}{x}&<& \frac{ r^2 }{ 2 } \end{eqnarray}

はさみうちの原理により、以下の関係が求められた。 \begin{eqnarray} \lim_{x \to 0}\frac{S_2}{x} = \frac{ r^2 }{ 2 } \end{eqnarray}

切り取る中心角 $x$ は一周分の中心角 $2 \pi$ を $2n$ 等分した角度なので、 $\displaystyle x=\frac{ 2 \pi }{ 2 n }=\frac{\pi }{ n }$ を代入する。

\begin{eqnarray} \lim_{n \to \infty}\frac{S_2}{\frac{ \pi }{ n }} &=& \frac{ r^2 }{ 2 } \newline \lim_{n \to \infty}\frac{nS_2}{\pi } &=&\frac{ r^2 }{ 2 } \end{eqnarray}

両辺を $2\pi$ 倍する。

\begin{eqnarray} \lim_{n \to \infty}2nS_2&=&\pi r^2 \end{eqnarray}

ここで左辺は、円を $2n$ 等分した扇型の $S_2$ を、再度 $2n$ 倍したものなので、元の円の面積に等しい。半径 $r$ を持つ円の面積が $\pi r^2$ で表されることが導かれた。

A4の宇宙

数学と物理をA4ノートに収まる範囲で。