等躍度運動で分かるテイラー展開

テイラー展開の性質

無限回微分可能な任意の関数を、ある点の近傍では下記のようなべき級数で表してよい。これをテイラー展開と呼ぶ。

\begin{eqnarray}
f(x)&=&f(a)+f'(a)(x-a)+\frac{1}{2!} f''(a)(x-a)^2+\frac{1}{3!}f'''(a)(x-a)^3+\cdots\\
&=& \sum_{k=0}^{\infty}\frac{f^{(k)}(a)}{k!}(x-a)^k
\end{eqnarray}

以前導いた等躍度運動の式を用いて、テイラー展開の性質3つが成り立つ理由を説明する。

1. 色々な関数をの無限べき級数で表してもよい。
2. 項の係数はである。
3. べき級数は低次の項だけ計算すれば大体合っている。

等躍度運動の式の変形

 説明のため、3次のべき級数である等躍度運動の式を再掲する。

\begin{eqnarray}
f(t)=\frac{1}{6}j t^3+\frac{1}{2}a_0t^2+v_0t+x_0
\end{eqnarray}

昇べきの順に並びかえる。

\begin{eqnarray}
f(t)=x_0+v_0t+\frac{1}{2}a_0t^2+\frac{1}{6}j t^3
\end{eqnarray}

係数を階乗で表す。

\begin{eqnarray}
f(t)=\frac{1}{0!}x_0+\frac{1}{1!}v_0t+\frac{1}{2!}a_0t^2+\frac{1}{3!}j t^3
\end{eqnarray}

今まではでと考えていたが、においてと考えて式を書き直す。

\begin{eqnarray}
f(t)&=&\frac{1}{0!}x_0+\frac{1}{1!}v_0(t-a)+\frac{1}{2!}a_0(t-a)^2+\frac{1}{3!}j (t-a)^3\\
&=&\sum_{k=0}^{3}\frac{C_n}{k!}(t-a)^k
\end{eqnarray}

次数が無限でないことを除けば、等躍度運動の式とテイラー展開の式はとても良く似ていることが分かる。 

1. なぜ色々な関数をのべき級数で表していいのか

仮想的にテイラー展開でもを時間、を位置と考えてみると、一階微分は速度、二回微分は加速度、三回微分は躍度…に相当する。速度(一階微分)や加速度(二階微分)が最終位置(元の関数)にどのように影響するかを、物体の運動と同じように適用することで、色々な関数を近似できる。

「対象の関数はべき級数とは限らないのにそうしていいのか？」という疑問が残るが、テイラー展開には「無限回微分可能」かつ「が基準点から近い」という縛りがあるので、べき級数でなくとも初速度や初加速度からの影響は「自然な」(が1つの値に定まる)影響しか受けない、と言えるのである。（もし成り立たないとすればとが収束半径よりも離れているということ）

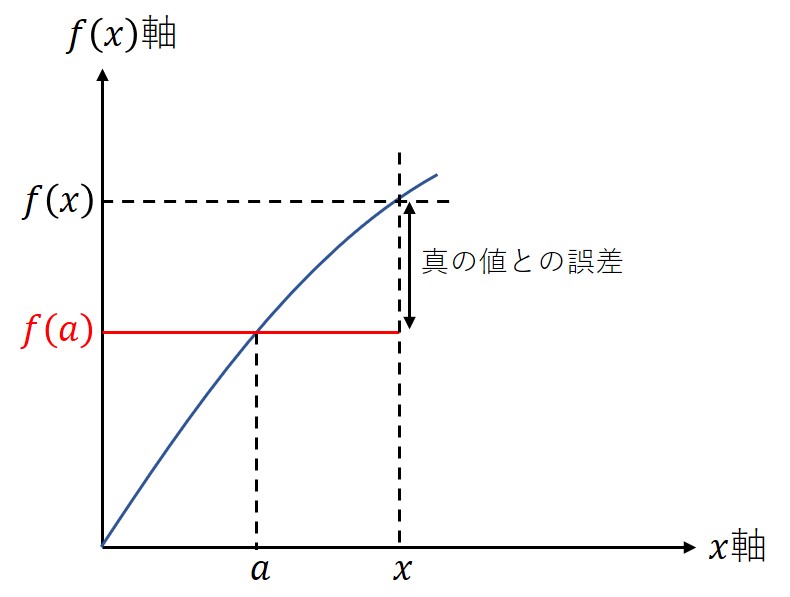
テイラー展開の手順を図字する。

ある関数において、をのべき級数で表したい。まずテイラー展開の基準点を決定する。

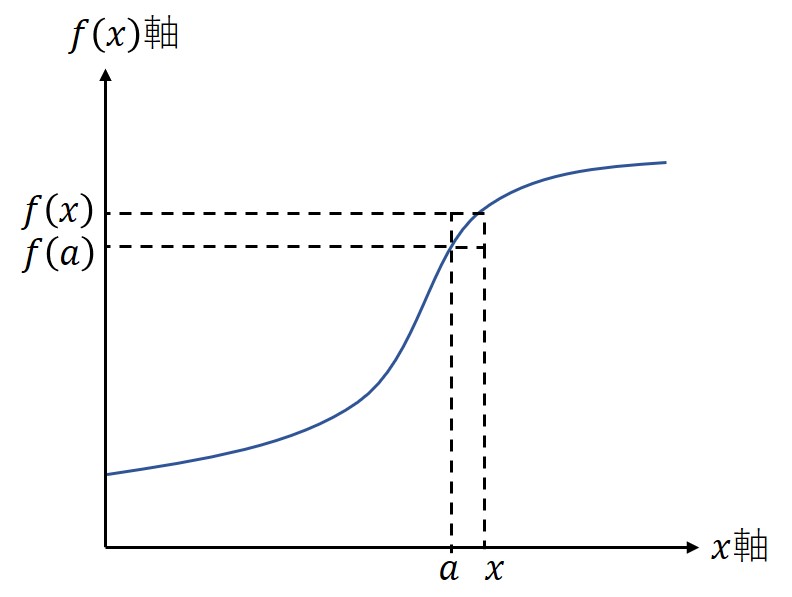
分かりやすいように目標地点を拡大する。とが近いという前提があるのでだけで近似してもそれなりに近い値になる。これは位置項だけによる近似と等価である。

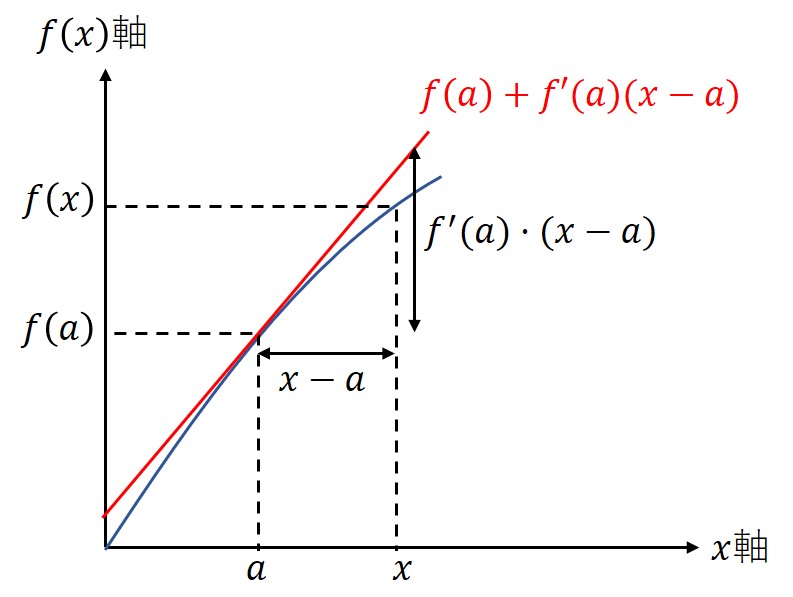
ここからがテイラー展開である。点における傾きに底辺長を掛けて先ほどのに加える。これは速度項による補正と等価であり、この処理で誤差がグッと小さくなることが分かる。テイラー展開のべき級数がの形になっているのは、この底辺長に対応していることによる。

さらに加速度項による近似を加える。この時の係数は視覚的に明らかではないので後述する。

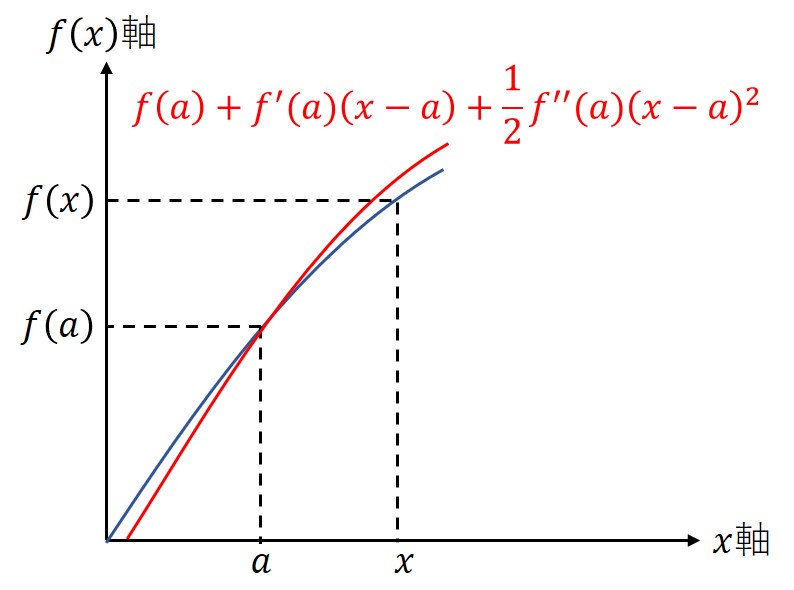
位置、速度、加速度と反映するごとに、だんだん誤差が小さくなっていることが分かる。

 2. なぜ項の係数はなのか

これについては先ほどの章でほぼ答えが出ている。等躍度運動の式を見れば、加速度項から距離を生むための係数は、躍度項から速度を生むための項はであった。このという係数は、回微分した項から距離を生むための係数に等しいのである。

3. なぜ途中まで計算すれば大体合っているのか

の強さ

等躍度運動の位置の式を再掲する。簡単のため、運動開始の時刻はとした。

\begin{eqnarray}
f(t)=\frac{1}{0!}x_0+\frac{1}{1!}v_0t+\frac{1}{2!}a_0t^2+\frac{1}{3!}j t^3
\end{eqnarray}

を代入してして位置を計算する。

\begin{eqnarray}
x &=& x_0+10v_0+ \frac{100}{2}a_0+\frac{1000}{6}j
\end{eqnarray}

係数にもよるが、がとても強いことが分かる。時間が経過するにつれて、位置の値はほとんど躍度項が占めることになる。

ここで逆にがとても小さい場合を考える。を代入して計算する。

\begin{eqnarray}
f(t)&=& x_0+ 0.1v_0+\frac{0.01}{2}a_0+\frac{0.001}{6}j
\end{eqnarray}

小さい時間においては、躍度項や加速度項はとても小さくなってしまい、速度項まで計算すれば大体の近似が可能になる。これがテイラー展開の本質の一つである。

項を拡張して無限のベキ関数を考える。これは躍度の時間変化率、そのまた時間変化率、と無限に考えていくことに等しい。は数列であり、項の比例係数が格納されている。

\begin{eqnarray}
x &=& x_0+v_0t+ \frac{1}{2}a_0t^2+\frac{1}{6}j t^3 +\cdots\\
&=& \frac{1}{0!}x_0+\frac{1}{1!}v_0t+ \frac{1}{2!}a_0t^2+\frac{1}{3!}j t^3 +\cdots\\
&=& \sum_{k=0}^{\infty} \frac{C_k}{k!}t^k
\end{eqnarray}

等躍度運動の場合、という訳である。