ln(x+1)のマクローリン展開と収束半径 その1
概要
基準点をとしたテイラー展開は特に有用なことがあり、マクローリン展開と呼ばれる。
のマクローリン展開を用いて、収束半径の概念を説明する。
導出
を基準にして
のテイラー展開を行う。
を微分して
を代入し、
を求める。
まずである。
一階微分
\begin{eqnarray}
f'(x)&=&\frac{1}{x+1}(x+1)'\\
&=&\frac{1}{x+1}\\
f'(0)&=&1\\
\end{eqnarray}
二階微分
\begin{eqnarray}
f''(x)&=&-\frac{1}{(x+1)^2}(x+1)'\\
&=&-\frac{1}{(x+1)^2}\\
f''(0)&=&-1\\
\end{eqnarray}
三階微分
\begin{eqnarray}
f'''(x)&=&\frac{2 \cdot 1}{(x+1)^3}(x+1)'\\
&=&\frac{2!}{(x+1)^3}\\
f'''(0)&=&2!\\
\end{eqnarray}
四階微分
\begin{eqnarray}
f''''(x)&=&-\frac{3\cdot2\cdot1}{(x+1)^4}(x+1)'\\
&=&-\frac{3!}{(x+1)^4}\\
f''''(0)&=&-3!\\
\end{eqnarray}
階微分
\begin{eqnarray}
f^{(n)}(x)&=&\frac{(-1)^{n-1} (n-1)!}{(x+1)^n}\\
f^{(n)}(0)&=&(-1)^{n-1} (n-1)!\\
\end{eqnarray}
計算したをマクローリン展開の式に代入する。
\begin{eqnarray}
f(x)&=&f(0)+f'(0)x+\frac{1}{2!}f''(0)x^2+\frac{1}{3!}f'''(0)x^3+\frac{1}{4!}f''''(0)x^4+\cdots\\
&=&0+x-\frac{1}{2}x^2+\frac{2!}{3!}x^3-\frac{3!}{4!}x^4+\cdots\\
&=&x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4+\cdots\\
&=&\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}x^n
\end{eqnarray}
綺麗にまとまった。
確認
元の関数とマクローリン展開された
および
を重ねてプロットしてみる。無限次までは扱えないので5次までと、13次までの2つの和を用いた。
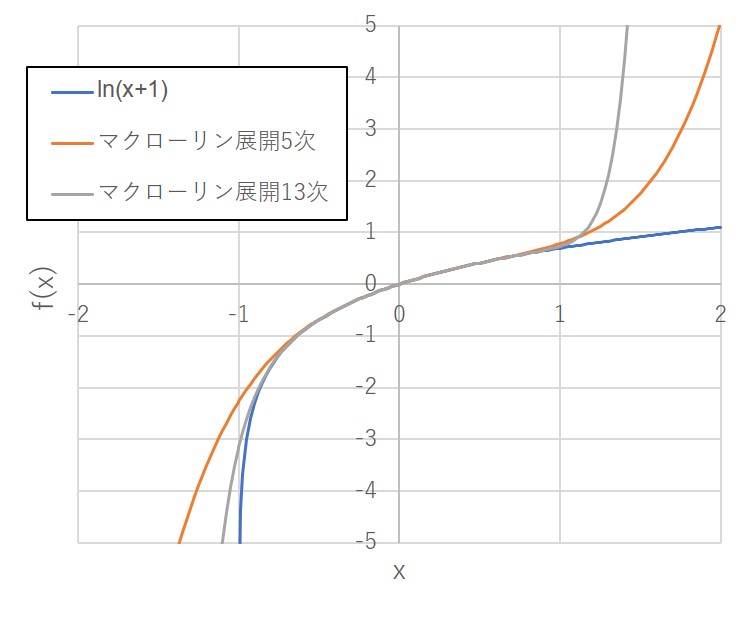
2つのマクローリン展開のグラフはの領域でよい近似が得られているが、
と
では明らかに発散している。また、これはテイラー展開の次数を増やしてもよくならず、むしろ急激に発散するようになることが分かる。
このテイラー級数が収束する領域がテイラー展開が成り立つ領域を表し、
を中心として
の幅を持つことから、「収束半径が
である」と呼ぶ。
また、ちょうどで収束するかどうかはまだ明らかでないことに注意。
この収束半径はダランベールの判定法で導出可能である。次回、その計算をやっていく。