ln(x+1)のマクローリン展開と収束半径 その2
概要
前回に続いて、のマクローリン展開(
を基準としたテイラー展開)を計算する。
をマクローリン展開すると以下のようなべき級数で表せることを前回示した。
\begin{eqnarray}
f(x)&=&x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4+\cdots\\
&=&\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n}x^n
\end{eqnarray}
収束半径の導出
、
であるので、判定式は以下のように書ける。
\begin{eqnarray} \require{cancel}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|{a_n}|}&=&\lim_{n \to \infty} \frac{ \left| \frac{(-1)^n}{n+1} \right|}{ \left| \frac{(-1)^{n-1}}{n} \right|}\\
&=&\lim_{n \to \infty} \left| \frac{(-1)^n n }{ (-1)^{n-1} (n+1) }\right| \\
&=&\lim_{n \to \infty} \left| \frac{ (-1)^\cancel{n} n }{ \cancel{(-1)^{n-1}} (n+1) }\right|\\
&=&\lim_{n \to \infty} \left| \frac{ -1 }{ \left(1+\frac{1}{n} \right) }\right|\\
&=& |-1|\\
&=& 1
\end{eqnarray}
すなわち、判定値であり、べき級数
の収束半径は
である。
この結果はべき級数を実際にプロットした結果とも整合していることが分かる。
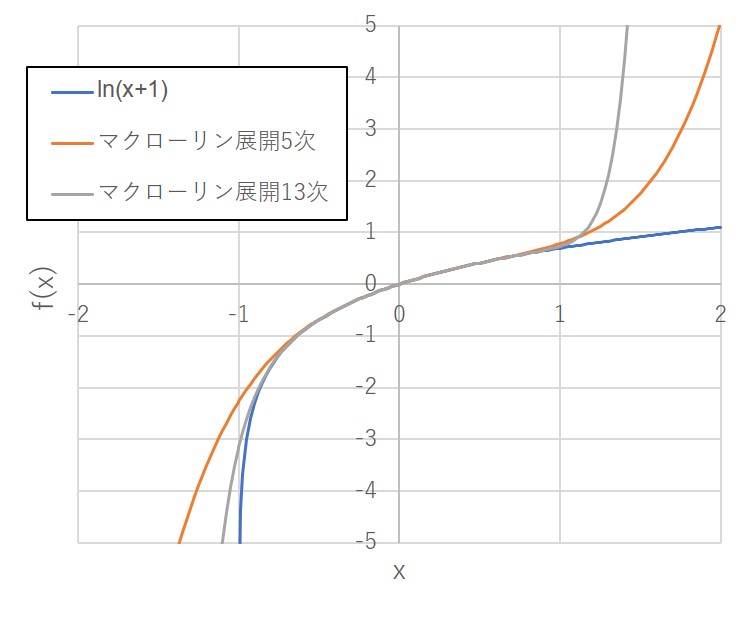
収束半径ちょうどの時
と
ちょうどの時に収束するか判定する。
の時、べき級数は以下のようになる。
\begin{eqnarray}
f(1)&=&1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots
\end{eqnarray}
これは交代調和級数であり、に収束する。
の時、べき級数は以下のようになる。
\begin{eqnarray}
f(-1)&=&-1-\frac{1}{2}-\frac{1}{3}-\frac{1}{4}-\cdots
\end{eqnarray}
これは全体にマイナスが付いた調和級数であるので、に発散する。
すなわち、をマクローリン展開した際の収束する
の範囲は、
であることが分かった。
(しかしに
を代入しても同様に
に発散するのだから、別に
を近似可能な領域に含めてもよい気もする)