xが0に近い時のsin xの性質、面積を用いる方法

概要

図のように、半径の円(緑)と、二つの直角三角形(青、赤)を考える。これらの直角三角形と、切り取られる扇形の面積を比較して、三角関数の微分に必要なを導出する。

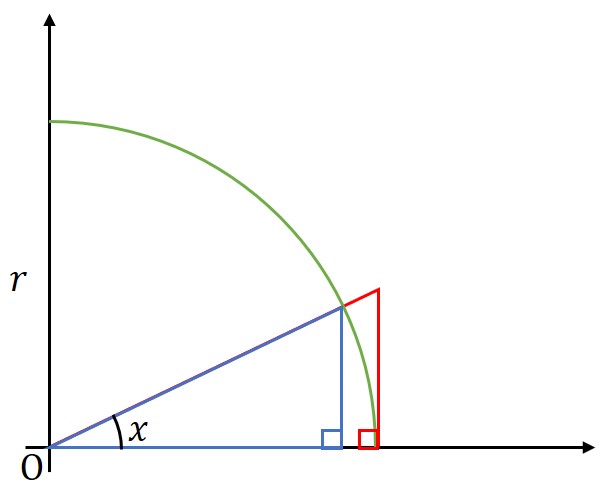
導出

まず二つの直角三角形と切り取られる扇形の面積を、円の半径と中心角を用いて表す。

小さな直角三角形の面積

斜辺がと定まることから底辺と高さを導ける。

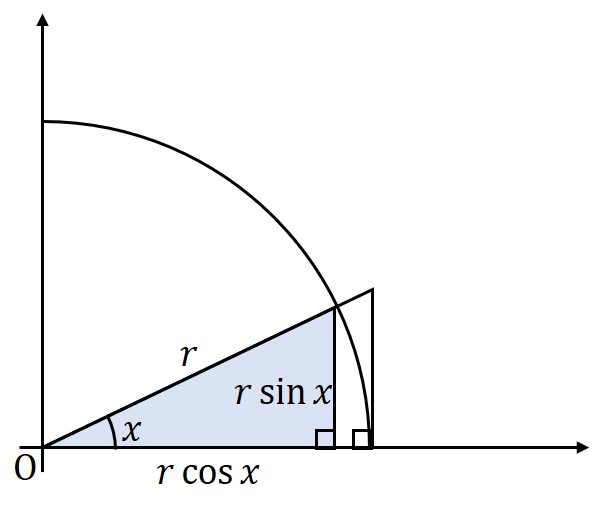
\begin{eqnarray}
S_1&=&\frac{1}{2}\times r \cos x \times r \sin x\\
&=&\frac{r^2 \sin x \cos x}{2}
\end{eqnarray}

切り取られる扇形の面積

円全体の面積に角度の割合をかけて求める。

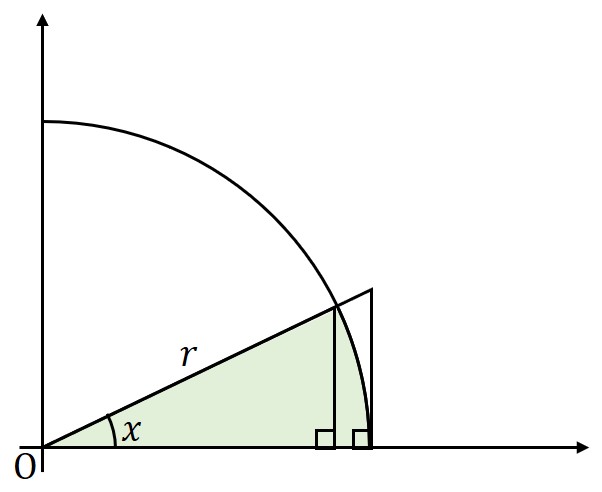
\begin{eqnarray}
S_2&=& \pi r^2 \times \frac{x}{2 \pi}\\
&=&\frac{r^2 x}{2}
\end{eqnarray}

大きな直角三角形の面積

底辺がと定まることから斜辺、高さの順に導ける。

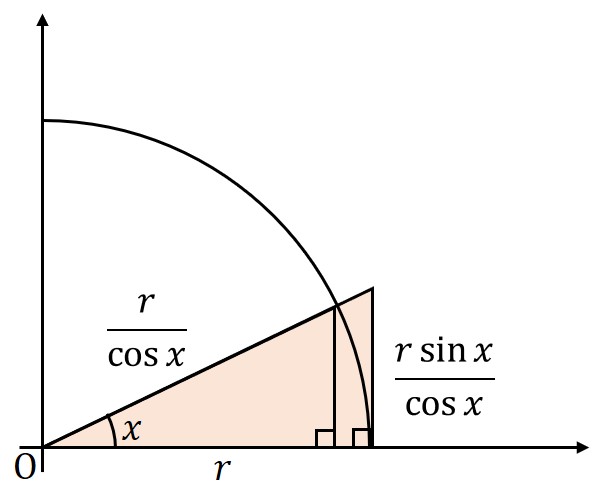
\begin{eqnarray}
S_3&=&\frac{1}{2} \times r \times \frac{r \sin x}{\cos x}\\
&=&\frac{r^2 \sin x}{2\cos x}
\end{eqnarray}

図を比較すると明らかに以下の関係が成り立つ。

\begin{eqnarray}
S_1<S_2<S_3
\end{eqnarray}

に計算した値を代入する。

\begin{eqnarray}
\frac{r^2 \sin x \cos x}{2}<\frac{r^2 x}{2}<\frac{r^2 \sin x}{2\cos x}
\end{eqnarray}

共通部分を打ち消す。
\begin{eqnarray} \require{cancel}
\frac{\cancel{r^2} \sin x \cos x}{\cancel{2}}&<&\frac{\cancel{r^2} x}{\cancel{2}}&<&\frac{\cancel{r^2} \sin x }{\cancel{2}\cos x}\\
\sin x \cos x&<&x&<&\frac{\sin x }{\cos x}
\end{eqnarray}

全体をで割る。としているので不等号の向きは変わらない。
\begin{eqnarray}
\cos x&<&\frac{x}{\sin x}&<&\frac{1}{\cos x}
\end{eqnarray}

全体の逆数を取る。不等号の向きが逆になる。
\begin{eqnarray}
\frac{1}{\cos x}&>&\frac{\sin x}{x}&>&\cos x
\end{eqnarray}

全体のを取る。

\begin{eqnarray}
\lim_{x \to 0}\frac{1}{\cos x}&>&\lim_{x \to 0}\frac{\sin x}{x}&>&\lim_{x \to 0}\cos x\\
1&>&\lim_{x \to 0}\frac{\sin x}{x}&>&1
\end{eqnarray}

はさみうちの原理により、以下の関係が求められた。

\begin{eqnarray}
\lim_{x \to 0}\frac{\sin x}{x}=1
\end{eqnarray}

またの時も、横軸の下側に2つの直角三角形と扇形を考えることができるので、この関係は同様に成り立つ。