余弦定理の証明(鋭角に対向する辺の場合)

概要

任意のにおいて、角に対向する辺の長さをを用いて表し、以下に表される余弦定理を証明する。

\begin{eqnarray}
c^2=a^2+b^2-2ab \cos C
\end{eqnarray}

導出

今回は図のように、が鋭角の場合を考える。

点から辺に垂線を引き、補助線とする。交点をとする。

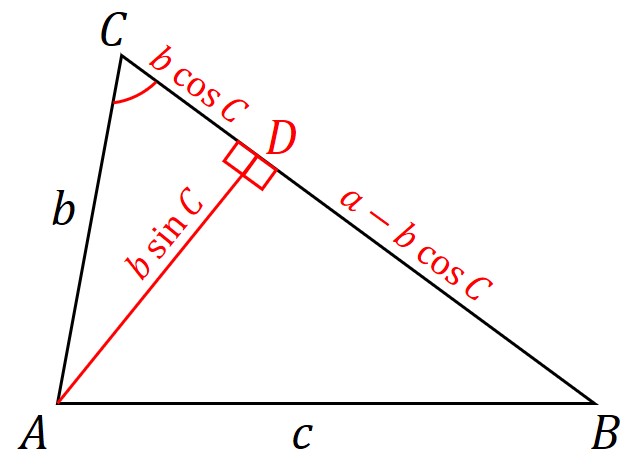
と辺を用いて、上図のようにとがわかる。また、なのでと表せる。

はを斜辺とする直角三角形であるので、三平方の定理より以下の関係が成り立つ。

\begin{eqnarray}
c^2&=&(b \sin C)^2 +(a-b\cos C)^2\\
&=& b^2 \sin^2 C+a^2-2ab \cos C +b^2 \cos ^2 C\\
&=&a^2+b^2(\sin ^2 C+ \cos ^2 C)-2ab \cos C\\
&=&a^2+b^2-2ab \cos C\\
\end{eqnarray}

を用いて、余弦定理が導かれた。