一次元の熱方程式を導く
概要
十分細く、一次元とみなせる針金の温度分布と、その経時変化を考えたい。まず解くべき微分方程式を導出する。
針金上の座標を、時間を
、温度を
とする。

また、熱の流れを考える。
導出
熱の流れについての式
熱の流れは温度の勾配
に比例する。(フーリエの法則)
この関係は以下のように式で表せる。
\begin{equation} \Gamma (x,t)=-k\frac{\partial}{ \partial x} T(x,t) \tag{1} \end{equation}
ここで、温度は
と
両方の関数としたので、偏微分になる。
は熱流の通りやすさを示す、熱伝導率と呼ばれる正の比例定数であり、針金の材質で決まる。熱は温度が高い方から低い方に流れるので、温度勾配とは逆方向に流れる。そのため
の前にマイナスがついている。
針金上の一次元区間を考える。
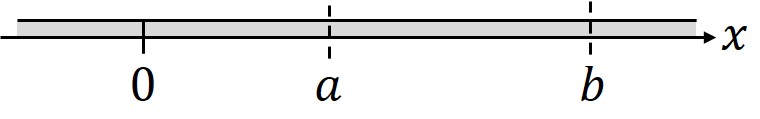
それぞれの点の熱流を式(1)形式で表す。
\begin{equation} \Gamma (a,t)=-k \left. \frac{\partial}{ \partial x} T(x,t)\right|_{x=a} \end{equation}
\begin{equation} \Gamma (b,t)=-k \left. \frac{\partial}{ \partial x} T(x,t)\right|_{x=b} \end{equation}
点と点
を通した熱流の出入りの総和は以下のように書ける。
\begin{equation} \Gamma(b,t)-\Gamma(a,t)=\int^b_a \frac{\partial}{\partial x} \Gamma(x,t) dx \tag{2} \end{equation}
式(2)を確認するため、右辺の定積分を実際にやってみよう。
\begin{eqnarray} 右辺&=&\int^b_a \frac{\partial}{\partial x} \Gamma(x,t) dx \\ &=&\bigl[\Gamma(x,t) \bigr]^b_a \\ &=&\Gamma(b,t)-\Gamma(a,t) \\ &=& 左辺 \end{eqnarray}
等式が確認された。
式2におよび
の中身を代入する。
\begin{eqnarray} −k\frac{∂}{∂x}T(x,t)|_{x=a}+k\frac{∂}{∂x}T(x,t)|_{x=b}=−k\int^b_a\frac{∂^2}{∂x^2}Γ(x,t)dx \end{eqnarray}
熱量についての式
一方、区間に蓄えられている熱量は以下のように書ける。
\begin{equation} Q(t)=c\int ^b_a T(x,t) dx \end{equation}
は物質の温まりにくさを示す正の比例定数であり、(単位長さ当たりの)熱容量と呼ばれる。値は針金の材質で決まる。
の時間変化を考える。両辺を
で微分する。ここで、
は
だけの関数なので全微分である。
\begin{eqnarray} \frac{d}{dt}Q(t)&=&c\frac{∂}{∂t}∫_a^b T(x,t) dx \\ &=& c∫_a^b \frac{∂}{∂t} T(x,t) dx \end{eqnarray}
二つの式を合体
熱量の保存則より以下の関係が成り立つ。
\begin{eqnarray} \frac{d}{dt} Q(t)=出入りする熱量の合計 \end{eqnarray}
左辺と右辺の中身はここまでに解っているので、それぞれ代入する。 \begin{eqnarray} c∫_a^b\frac{∂}{∂t} T(x,t) dx = k∫^b_a\frac{∂^2}{∂x^2} Γ(x,t) dx \end{eqnarray}
この関係が全てので成り立つためには積分の対象が等しい必要がある。
\begin{eqnarray}
c\frac{∂}{∂t}T(x,t)=k\frac{∂^2}{∂x^2}Γ(x,t)
\end{eqnarray}
一次元の熱方程式が導かれた。この微分方程式を解くことで、針金の温度分布とその時間変化が求められる。