sin xのマクローリン展開

概要

基準点をとしたテイラー展開は特に有用なことがあり、マクローリン展開と呼ばれる。のマクローリン展開を行う。

導出 

を微分してを代入し、を求める。

まずである。

一階微分

\begin{eqnarray}
f'(x)&=&\cos x\\
f'(0)&=&1\\
\end{eqnarray}

二階微分

\begin{eqnarray}
f''(x)&=&-\sin x\\
f''(0)&=&0\\
\end{eqnarray}

三階微分 
\begin{eqnarray}
f'''(x)&=&-\cos x\\
f'''(0)&=&-1\\
\end{eqnarray}

四階微分 
\begin{eqnarray}
f^{(4)}(x)&=&\sin x\\
f^{(4)}(0)&=&0\\
\end{eqnarray}

五階微分 
\begin{eqnarray}
f^{(5)}(x)&=&\cos x\\
f^{(5)}(0)&=&1\\
\end{eqnarray}

計算したをマクローリン展開の式に代入する。

\begin{eqnarray}
f(x)&=&f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\frac{f^{(4)}(0)}{4!}x^4+\frac{f^{(5)}(0)}{5!}x^5+\cdots\\
&=&0+1\cdot x+\frac{0}{2!}\cdot x^2+\frac{-1}{3!}x^3+\frac{0}{4!}x^4+\frac{1}{5!}x^5+\cdots\\
&=&x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots\\
\end{eqnarray}

となる項を飛ばし、の代わりに新たな変数を用いてを書き直す。

\begin{eqnarray}
f(x)&=&x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots\\
&=&\sum_{k=1}^{\infty}  \frac{(-1)^{k -1}}{(2k-1)!}x^{2k-1}\\
\end{eqnarray} 

綺麗にまとまった。

収束半径

導出式再計算

をマクローリン展開したべき級数の収束半径を導出する。しかし、今回は対象が通常のべき級数ではなく、奇数次の項だけを持つべき級数なので、導出式を再計算する必要がある。

奇数次べき数列をダランベールの判定式に代入して級数の収束判定を行う。

\begin{eqnarray} \require{cancel}
\lim_{k \to \infty} \frac{|a_{k+1}x^{2k+1}|}{|a_k x^{2k- 1}|}&<&1\\
\lim_{k \to \infty} \frac{|a_{k+1}x^{\cancelto{2}{2k+1}}|}{|a_k \cancel{x^{2k-1}}|}&<&1\\
\lim_{k \to \infty} \frac{|a_{k+1}|}{|a_k|}|x^2|&<&1\\
|x^2|\lim_{k \to \infty} \frac{|a_{k+1}|}{|a_k|}&<&1
\end{eqnarray}

分子と分母のが打ち消し合い、だけが残った。

と置いて両辺をで割る。は絶対値同士の商なので不等号の向きは変わらない。

\begin{eqnarray} \require{cancel}
|x^2|\lim_{k \to \infty} \frac{|a_{k+1}|}{|a_k|}&<&1\\
|x^2| L&<&1\\
|x^2| &<&\frac{1}{L}\\
-\frac{1}{\sqrt{L}}<x &<&\frac{1}{\sqrt{L}}\\
\end{eqnarray}

の取りうる範囲が定まった。収束半径はと表せる。あとはこのを求めればよい。

今回の式への適用

、である。これらの値を代入してを求める。
 

\begin{eqnarray} \require{cancel}
\lim_{k \to \infty} \frac{|a_{k+1}|}{|{a_k}|}&=&\lim_{k \to \infty} \frac{ \left| \frac{(-1)^{k }}{(2k+1)!} \right|}{ \left| \frac{(-1)^{k -1}}{(2k-1)!} \right|}\\
&=&\lim_{k \to \infty} \left| \frac{(-1)^k (2k-1)! }{ (-1)^{k -1} (2k+1)! }\right| \\
&=&\lim_{k \to \infty} \left| \frac{(-1)^\cancel{k} (2k-1)! }{ \cancel{(-1)^{k -1}} (2k+1)! }\right| \\
&=&\lim_{k \to \infty} \left| \frac{ -1 }{ (2k+1)2k }\right|\\
&=& 0
\end{eqnarray}

すなわち、判定値であり、収束半径はである。

これはマクローリン展開の次数が十分大きければ、どのようなにおいても収束させることができることを意味する。本質的にと表してよいのである。

確認

元の関数と、マクローリン展開した級数を5次と13次まで重ねてプロットした。ln(x+1)のマクローリン展開とは異なり、次数を増加させると収束する領域がどんどん広がっていき、収束半径が無限大であることと対応している。

交代調和級数の収束判定

概要

調和級数の正負が1項ごとに入れ替わる、交代調和級数の収束判定を行う。

全項がプラスの調和級数は無限大に発散してしまったが、これは半分の項がマイナスなので、より収束しやすい級数と言える。

導出

足し合わされる数列の一般項をと書き、級数を代数的に表す。

\begin{eqnarray}
\sum_{k=1}^{\infty} a_k&=&1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots\\
&=&\sum_{k=1}^{\infty} \frac{(-1)^{k - 1}}{k}
\end{eqnarray}

1項目から項目までの部分和を実際にプロットしてみると図のようになり、の増加に伴って明らかにある値に収束していく。この収束値はいくつになるだろうか。

収束値を導出するにあたっての部分が邪魔なので、級数を以下のように変形する。最後にをとれば目的の級数が得られる。

\begin{eqnarray}
\sum_{k=1}^{2n} \frac{(-1)^{k - 1}}{k} = \sum_{k=1}^n \frac{1}{n+k}
\end{eqnarray}

この式変形は以下のようになる。左辺を式変形して右辺を目指す。

を左辺に足し、そして引いても合計は変化しない。(なぜこんな変形をするかは後で分かる)

\begin{eqnarray}
\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}&=&\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}+\underline{2\sum_{k=1}^n\frac{1}{2k}-2\sum_{k=1}^n\frac{1}{2k}}
\end{eqnarray}

カッコで右辺2項目までをくくり、右辺3項目を約分する。
\begin{eqnarray} \require{cancel}
\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}&=&\left(\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}+2\sum_{k=1}^n\frac{1}{2k}\right)-2\sum_{k=1}^n\frac{1}{2k}\\
&=&\left(\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}+2\sum_{k=1}^n\frac{1}{2k}\right)-\cancel{2}\sum_{k=1}^n\frac{1}{\cancel{2}k}\\
&=&\left(\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}+2\sum_{k=1}^n\frac{1}{2k}\right)-\sum_{k=1}^n\frac{1}{k}
\end{eqnarray}

右辺カッコ内を計算するとどうなるだろうか。

• 右辺第一項

\begin{eqnarray}
\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}=\frac{1}{1}-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots\\
\end{eqnarray}

• 右辺第二項

\begin{eqnarray}
2\sum_{k=1}^n\frac{1}{2k}=2\cdot\frac{1}{2}+2\cdot\frac{1}{4}+2\cdot\frac{1}{6}\cdots
\end{eqnarray}

これらを辺々足すと、マイナスの項だけをプラスの2倍の項が貫通して、ちょうど調和級数の形になるのである。

• 合計

\begin{eqnarray}
\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}+2\sum_{k=1}^n\frac{1}{2k}&=&\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots\\
&=&\sum_{k=1}^{2n}\frac{1}{k}
\end{eqnarray}

計算したカッコの中身を代入する。
\begin{eqnarray}
\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}&=&\left(\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}+2\sum_{k=1}^n\frac{1}{2k}\right)-\sum_{k=1}^n\frac{1}{k}\\
&=&\sum_{k=1}^{2n}\frac{1}{k}-\sum_{k=1}^n\frac{1}{k}\\
\end{eqnarray}

この右辺第2項の和は、第1項の和の最初の項を相殺する。
\begin{eqnarray}
\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}&=&\sum_{k=1}^{2n}\frac{1}{k}-\sum_{k=1}^n\frac{1}{k}\\
&=&\sum_{k=n+1}^{2n} \frac{1}{k}\\
\end{eqnarray}

和を取る領域がからまでになるように書き直し、式変形が完了した。

\begin{eqnarray}
\sum_{k=1}^{2n}\frac{(-1)^{k - 1}}{k}&=&\sum_{k=n+1}^{2n} \frac{1}{k}\\
&=&\underline{\sum_{k=1}^n \frac{1}{n+k}}
\end{eqnarray}

区分求積法を用いて、変形した式の無限和を計算する。

\begin{eqnarray}
\lim_{n \to \infty}\sum_{k=1}^{n}\frac{1}{n+k}&=&\lim_{n\to \infty}\frac{1}{n}\sum_{k=1}^n\frac{1}{1+\frac{k}{n}}\\
&=&\int_0^1\frac{1}{1+x}dx\\
&=&\biggl[\ln{(1+x)}\biggr]^1_0\\
&=&\ln 2\\
&=&0.6931\cdots\\
\end{eqnarray}

収束値が求められた。最初にプロットしたグラフとも整合していることが分かる。

交代調和級数を構成する値は全て分数なので明らかに有理数だが、その無限和は無理数であるに収束するのである。

ln(x+1)のマクローリン展開と収束半径 その2

概要

前回に続いて、のマクローリン展開(を基準としたテイラー展開)を計算する。

をマクローリン展開すると以下のようなべき級数で表せることを前回示した。

\begin{eqnarray}
f(x)&=&x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4+\cdots\\
&=&\sum_{n=1}^{\infty}  \frac{(-1)^{n-1}}{n}x^n
\end{eqnarray}

収束半径の導出

をマクローリン展開したべき級数の収束半径を導出する。

、であるので、判定式は以下のように書ける。

\begin{eqnarray} \require{cancel}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|{a_n}|}&=&\lim_{n \to \infty} \frac{ \left| \frac{(-1)^n}{n+1} \right|}{ \left| \frac{(-1)^{n-1}}{n} \right|}\\
&=&\lim_{n \to \infty} \left| \frac{(-1)^n n }{ (-1)^{n-1} (n+1) }\right| \\
&=&\lim_{n \to \infty} \left| \frac{ (-1)^\cancel{n} n }{ \cancel{(-1)^{n-1}} (n+1) }\right|\\
&=&\lim_{n \to \infty} \left| \frac{ -1 }{ \left(1+\frac{1}{n} \right) }\right|\\
&=& |-1|\\
&=& 1
\end{eqnarray}

すなわち、判定値であり、べき級数の収束半径はである。

この結果はべき級数を実際にプロットした結果とも整合していることが分かる。

収束半径ちょうどの時

とちょうどの時に収束するか判定する。

の時、べき級数は以下のようになる。

\begin{eqnarray}
f(1)&=&1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots
\end{eqnarray}

これは交代調和級数であり、に収束する。

の時、べき級数は以下のようになる。

\begin{eqnarray}
f(-1)&=&-1-\frac{1}{2}-\frac{1}{3}-\frac{1}{4}-\cdots
\end{eqnarray}

これは全体にマイナスが付いた調和級数であるので、に発散する。

すなわち、をマクローリン展開した際の収束するの範囲は、であることが分かった。

(しかしにを代入しても同様にに発散するのだから、別にを近似可能な領域に含めてもよい気もする)

収束半径の導出

概要

ダランベールの収束判定法を使ってテイラー展開の収束半径を計算する。

ダランベールの収束判定法(再掲)

級数が収束するかどうか、以下の式で判定できる。

• 足し合わされる数列が以下の条件を満たすとき、級数は収束する。

\begin{eqnarray}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} < 1
\end{eqnarray}

• が以下の条件を満たすとき、級数は発散する。

\begin{eqnarray}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} > 1
\end{eqnarray}

• が以下の条件を満たすときは、収束することも発散することもあり、判定できない。

\begin{eqnarray}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} = 1
\end{eqnarray}

成り立つ原理はこちらを参照。

べき級数への適用

各にがかかった、べき級数の収束判定を行う。このはテイラー展開の基準点である。

べき数列を判定式に代入する。

\begin{eqnarray} \require{cancel}
\lim_{n \to \infty} \frac{|a_{n+1}(x-a)^{n+1}|}{|a_n (x-a)^{n}|}&<&1\\
\lim_{n \to \infty} \frac{|a_{n+1}(x-a)^{\cancel{n+1}}|}{|a_n \cancel{(x-a)^{n}}|}&<&1\\
\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|}|x-a|&<&1\\
\end{eqnarray}

分子と分母のが打ち消し合い、だけが残った。

はもはやに関係ないのでの外に出してしまう。 

\begin{eqnarray} \require{cancel}
|x-a|\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|}&<&1
\end{eqnarray}

べき級数の収束条件が求められた。

収束半径

がどんな値ならば収束条件を満たすだろうか。

ここでをと置く。

\begin{eqnarray} \require{cancel}
|x-a|\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|}&<&1\\
|x-a|L&<&1
\end{eqnarray}

不等式の両辺をで割る。(は絶対値同士の商なので正の値であり、不等号の向きは変わらない。)

\begin{eqnarray} \require{cancel}
|x-a|&<&\frac{1}{L}
\end{eqnarray}

最後に不等式を絶対値無しで書き直す。

\begin{eqnarray} \require{cancel}
-\frac{1}{L}<x-a<\frac{1}{L}
\end{eqnarray}

収束のためにがとりうる値が示された。が収束半径を表す。 

マクローリン展開ではであるので、以下のようになる。

\begin{eqnarray} \require{cancel}
-\frac{1}{L}<x<\frac{1}{L}
\end{eqnarray} 

ln(x+1)のマクローリン展開の収束領域がであったことと整合していることが分かる。

はもともと、べき級数でない級数をダランベールの収束判定式に代入した値であった。それが分母に来ているので、「足される数列が高速に収束するならば、が小さくなり、の取りうる値が広い」という関係になっている。 

ln(x+1)のマクローリン展開と収束半径 その1

概要

基準点をとしたテイラー展開は特に有用なことがあり、マクローリン展開と呼ばれる。のマクローリン展開を用いて、収束半径の概念を説明する。

導出 

を基準にしてのテイラー展開を行う。

を微分してを代入し、を求める。

まずである。

一階微分

\begin{eqnarray}
f'(x)&=&\frac{1}{x+1}(x+1)'\\
&=&\frac{1}{x+1}\\
f'(0)&=&1\\
\end{eqnarray}

二階微分

\begin{eqnarray}
f''(x)&=&-\frac{1}{(x+1)^2}(x+1)'\\
&=&-\frac{1}{(x+1)^2}\\
f''(0)&=&-1\\
\end{eqnarray}

三階微分 
\begin{eqnarray}
f'''(x)&=&\frac{2 \cdot 1}{(x+1)^3}(x+1)'\\
&=&\frac{2!}{(x+1)^3}\\
f'''(0)&=&2!\\
\end{eqnarray}

四階微分 
\begin{eqnarray}
f''''(x)&=&-\frac{3\cdot2\cdot1}{(x+1)^4}(x+1)'\\
&=&-\frac{3!}{(x+1)^4}\\
f''''(0)&=&-3!\\
\end{eqnarray}

階微分 
\begin{eqnarray}
f^{(n)}(x)&=&\frac{(-1)^{n-1} (n-1)!}{(x+1)^n}\\
f^{(n)}(0)&=&(-1)^{n-1} (n-1)!\\
\end{eqnarray}

計算したをマクローリン展開の式に代入する。

\begin{eqnarray}
f(x)&=&f(0)+f'(0)x+\frac{1}{2!}f''(0)x^2+\frac{1}{3!}f'''(0)x^3+\frac{1}{4!}f''''(0)x^4+\cdots\\
&=&0+x-\frac{1}{2}x^2+\frac{2!}{3!}x^3-\frac{3!}{4!}x^4+\cdots\\
&=&x-\frac{1}{2}x^2+\frac{1}{3}x^3-\frac{1}{4}x^4+\cdots\\
&=&\sum_{n=1}^{\infty}  \frac{(-1)^{n-1}}{n}x^n
\end{eqnarray}

綺麗にまとまった。

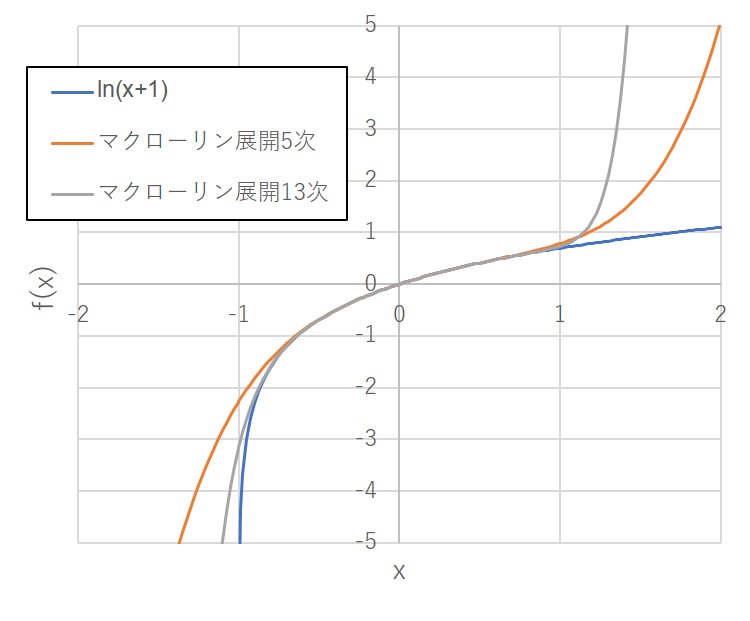
確認

元の関数とマクローリン展開されたおよびを重ねてプロットしてみる。無限次までは扱えないので5次までと、13次までの2つの和を用いた。

2つのマクローリン展開のグラフはの領域でよい近似が得られているが、とでは明らかに発散している。また、これはテイラー展開の次数を増やしてもよくならず、むしろ急激に発散するようになることが分かる。

このテイラー級数が収束する領域がテイラー展開が成り立つ領域を表し、を中心としての幅を持つことから、「収束半径がである」と呼ぶ。

また、ちょうどで収束するかどうかはまだ明らかでないことに注意。

この収束半径はダランベールの判定法で導出可能である。次回、その計算をやっていく。

収束判定の例題

例題

を収束判定し、収束するならその値を求める。

この足し合わされる数列はでいきなり無限大に発散してしまうのでからの和とした。

調和級数の収束判定

の無限和、が収束するか考える。この無限和は調和級数と呼ばれる。

この数列は、明らかにを増加させるとだんだん小さくなっていくが、項を無限に足したら発散するかも知れない。

ダランベールの判定法

まずダランベールの判定法で収束するかを判定してみる。

\begin{eqnarray}
\lim_{n \to \infty}\frac{|a_{n+1}|}{|a_n|}&=& \lim_{n \to \infty}\frac{\frac{1}{n+1}}{\frac{1}{n}}\\
&=&\lim_{n \to \infty}\frac{n}{n+1}\\
&=&\lim_{n \to \infty}\frac{1}{1+\frac{1}{n}}\\
&=&1
\end{eqnarray}

分子と分母をで割ると判定式はに等しくなり、収束するとも発散するとも言い切れない。そのため別の方法で収束するか判定する必要がある。

比較判定法

比較判定法で下から抑える作戦で行く。

の無限和を書き下す。

\begin{eqnarray}
\sum_{n=1}^{\infty} a_n=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\cdots
\end{eqnarray}

明らかにより小さい別の数列の和を考える。

\begin{eqnarray}
\sum_{n=1}^{\infty}b_n=\underline{\frac{1}{1}}+\underline{\frac{1}{2}}+\frac{1}{4}+\underline{\frac{1}{4}}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\underline{\frac{1}{8}}+\frac{1}{16}+\cdots
\end{eqnarray}

は項目の後に、項の大きさをするような数列である。アンダーラインが引かれた項はと等しく、引かれていない項はより小さい。

そのため以下の不等式が成り立つ。

\begin{eqnarray}
\sum_{n=1}^{\infty} a_n > \sum_{n=1}^{\infty}b_n
\end{eqnarray}

さらに、並んだ同一の分数は以下のようにまとめることができる。

\begin{eqnarray}
\sum_{k=1}^{\infty}b_n=\underline{\frac{1}{1}}+\frac{1}{2}+\overbrace{\frac{1}{4}+\frac{1}{4}}^{\frac{1}{2}}+\overbrace{\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}}^{\frac{1}{2}}+\overbrace{\frac{1}{16}+\cdots+\frac{1}{16}}^{\frac{1}{2}}+\cdots
\end{eqnarray}

すなわち、以下のように書ける。

\begin{eqnarray}
\sum_{k=1}^{\infty}b_n=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots 
\end{eqnarray}

この式よりの和は無限大に発散することが分かる。

そのため、以下の式が成り立つ。

\begin{equation}
\underline{\sum_{n=1}^{\infty} a_n > \sum_{n=1}^{\infty}b_n=\infty}
\end{equation}

この関係より、より大きいも無限大に発散することが分かる。

ゼータ関数との関係

ゼータ関数は以下の形で定義される。

\begin{equation}
\zeta(s)=\sum_{k=1}^{\infty}\frac{1}{k^s}
\end{equation}

すなわち、は調和級数に等しいので、やはり無限大に発散する。

\begin{equation}
\zeta(1)=\sum_{k=1}^{\infty}\frac{1}{k^1}=\infty
\end{equation}