A4の宇宙

数学と物理をA4ノートに収まる範囲で。

e^xのマクローリン展開

数学 数列

目次に戻る

概要

基準点をx=0としたテイラー展開は特に有用なことがあり、マクローリン展開と呼ばれる。 e^xのマクローリン展開を行う。

 

導出 

f(x)=e^xを微分してx=0を代入し、f^{(n)}(0)を求める。

まずf(0)=e^0=1である。

 

一階微分

\begin{eqnarray}
f'(x)&=&e^x\\
f'(0)&=&1\\
\end{eqnarray}

 

二階微分

\begin{eqnarray}
f''(x)&=&e^x\\
f''(0)&=&1\\
\end{eqnarray}

 

三階微分 
\begin{eqnarray}
f'''(x)&=&e^x\\
f'''(0)&=&1\\
\end{eqnarray}

 

四階微分 
\begin{eqnarray}
f^{(4)}(x)&=&e^x\\
f^{(4)}(0)&=&1\\
\end{eqnarray}

 

計算したf^{(n)}(0)をマクローリン展開の式に代入する。

\begin{eqnarray}
f(x)&=&f(0)+f'(0)x+\frac{f''(0)}{2!}x^2+\frac{f'''(0)}{3!}x^3+\frac{f^{(4)}(0)}{4!}x^4+\cdots\\
&=&1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+\cdots\\
&=& \sum_{k=0}^\infty \frac{1}{k!}x^k
\end{eqnarray}

 

綺麗にまとまった。

 

収束半径

e^xをマクローリン展開したべき級数の収束半径を導出する。

\displaystyle a_k=\frac{1}{k!}、 \displaystyle a_{k+1}=\frac{1}{(k+1)!}である。これらの値を代入して \displaystyle L=\lim_{k \to \infty} \frac{|a_{k+1}|}{|{a_k}|}を求める。
 

\begin{eqnarray} \require{cancel}
\lim_{k \to \infty} \frac{|a_{k+1}|}{|{a_k}|}&=&\lim_{k \to \infty} \frac{ \left| \frac{1}{(k+1)!} \right|}{ \left| \frac{1}{k!} \right|}\\
&=&\lim_{k \to \infty} \left| \frac{k!}{ (k+1)! }\right| \\
&=&\lim_{k \to \infty} \left| \frac{\cancel{k!}}{ (k+1)\cancel{!} }\right| \\
&=&\lim_{k \to \infty} \left| \frac{ 1 }{ (k+1) }\right|\\
&=& 0
\end{eqnarray}

 

 

すなわち、判定値L=0であり、収束半径は \displaystyle \frac{1}{\sqrt{L}}=\frac{1}{0}=\inftyである。

 

これはマクローリン展開の次数が十分大きければ、どのようなxにおいても収束させることができることを意味する。本質的に \displaystyle e^x=1+x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+\frac{1}{4!}x^4+\cdotsと表してよいのである。

 

確認

f:id:dai-ig:20190223144551j:plain

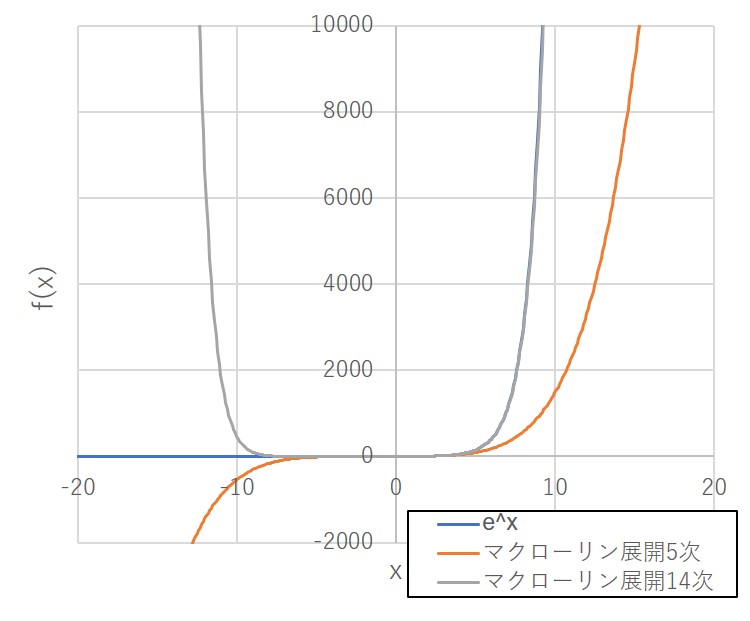
f(x)=e^xとマクローリン展開された級数をプロットした。 \displaystyle \lim_{x \to -\infty} e^xは0に収束するが、べき級数では次数によって \pm \inftyに発散してしまう。しかし次数が増えると徐々に収束する領域が増えていくことが分かる。これが収束半径\inftyと対応している。