調和級数の収束判定

の無限和、が収束するか考える。この無限和は調和級数と呼ばれる。

この数列は、明らかにを増加させるとだんだん小さくなっていくが、項を無限に足したら発散するかも知れない。

ダランベールの判定法

まずダランベールの判定法で収束するかを判定してみる。

\begin{eqnarray}
\lim_{n \to \infty}\frac{|a_{n+1}|}{|a_n|}&=& \lim_{n \to \infty}\frac{\frac{1}{n+1}}{\frac{1}{n}}\\
&=&\lim_{n \to \infty}\frac{n}{n+1}\\
&=&\lim_{n \to \infty}\frac{1}{1+\frac{1}{n}}\\
&=&1
\end{eqnarray}

分子と分母をで割ると判定式はに等しくなり、収束するとも発散するとも言い切れない。そのため別の方法で収束するか判定する必要がある。

比較判定法

比較判定法で下から抑える作戦で行く。

の無限和を書き下す。

\begin{eqnarray}
\sum_{n=1}^{\infty} a_n=\frac{1}{1}+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}+\frac{1}{9}+\cdots
\end{eqnarray}

明らかにより小さい別の数列の和を考える。

\begin{eqnarray}
\sum_{n=1}^{\infty}b_n=\underline{\frac{1}{1}}+\underline{\frac{1}{2}}+\frac{1}{4}+\underline{\frac{1}{4}}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\underline{\frac{1}{8}}+\frac{1}{16}+\cdots
\end{eqnarray}

は項目の後に、項の大きさをするような数列である。アンダーラインが引かれた項はと等しく、引かれていない項はより小さい。

そのため以下の不等式が成り立つ。

\begin{eqnarray}
\sum_{n=1}^{\infty} a_n > \sum_{n=1}^{\infty}b_n
\end{eqnarray}

さらに、並んだ同一の分数は以下のようにまとめることができる。

\begin{eqnarray}
\sum_{k=1}^{\infty}b_n=\underline{\frac{1}{1}}+\frac{1}{2}+\overbrace{\frac{1}{4}+\frac{1}{4}}^{\frac{1}{2}}+\overbrace{\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}}^{\frac{1}{2}}+\overbrace{\frac{1}{16}+\cdots+\frac{1}{16}}^{\frac{1}{2}}+\cdots
\end{eqnarray}

すなわち、以下のように書ける。

\begin{eqnarray}
\sum_{k=1}^{\infty}b_n=1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots 
\end{eqnarray}

この式よりの和は無限大に発散することが分かる。

そのため、以下の式が成り立つ。

\begin{equation}
\underline{\sum_{n=1}^{\infty} a_n > \sum_{n=1}^{\infty}b_n=\infty}
\end{equation}

この関係より、より大きいも無限大に発散することが分かる。

ゼータ関数との関係

ゼータ関数は以下の形で定義される。

\begin{equation}
\zeta(s)=\sum_{k=1}^{\infty}\frac{1}{k^s}
\end{equation}

すなわち、は調和級数に等しいので、やはり無限大に発散する。

\begin{equation}
\zeta(1)=\sum_{k=1}^{\infty}\frac{1}{k^1}=\infty
\end{equation}

ダランベールの収束判定法

概要

ある数列を考えたとき、その級数(=無限和)は無限大に発散するのか、それともある値に収束するのかを確認したい。どうすればよいか？

\begin{eqnarray}
\sum_{k=1}^{\infty}a_n
\end{eqnarray}

結論から言えば、数列が以下の条件を満たすとき、級数はどこかの値に収束する。

\begin{eqnarray}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} < 1
\end{eqnarray}

以下の条件を満たすとき、級数は発散する。

\begin{eqnarray}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} > 1
\end{eqnarray}

以下の条件を満たすときは、収束することも発散することもあり、判定できない。

\begin{eqnarray}
\lim_{n \to \infty} \frac{|a_{n+1}|}{|a_n|} = 1
\end{eqnarray}

導出

これは単純に「が大きい時にだんだんが小さくなる傾向にある級数は収束する」と言っているように見えるが、実際には調和級数など、その傾向にあっても発散する級数はある。

ダランベールの判定法は等比数列の和と比較することにより、収束の判定を行っているのである。

等比数列の和の公式を再掲する。

\begin{equation}
\sum_{k=0}^nr^ka_0=\frac{a_0(1-r^{n+1})}{1-r}
\end{equation}

この式は明らかにの時収束し、の時に無限大に発散する。

すなわち、「公比の絶対値が1より小さい等比数列は収束する」「公比の絶対値が1より大きい等比数列は発散する」ということは代数的に明らかである。

ダランベールの判定法に用いたという式は、において公比の絶対値に相当する値を探ることに他ならない。

この仮想的な公比の絶対値が1を下回るとき、この級数はの等比級数よりも小さいので、収束することが分かるのである。

逆に、仮想公比の絶対値が1を上回れば、の等比級数よりも大きいので、発散することが分かる。

例題

級数が収束するか判定する。

ダランベールの判定法を用いて

\begin{eqnarray} \require{cancel}
\lim_{n \to \infty} \frac{ \left| \frac{2^{n+1}}{(n+1)!} \right| }{\left| \frac{2^{n}}{n!} \right| }&=&\lim_{n \to \infty} \frac{2^{n+1}n!}{2^n (n+1)!}\\
&=&\lim_{n \to \infty} \frac{2^{\cancel{n}+1}\xcancel{n!}}{\cancel{2^n} (n+1)\xcancel{!}}\\
&=&\lim_{n \to \infty} \frac{2}{n+1}\\
&=& 0
\end{eqnarray}

判定式がより小さくなったので、この級数は収束する。

等躍度運動で分かるテイラー展開

テイラー展開の性質

無限回微分可能な任意の関数を、ある点の近傍では下記のようなべき級数で表してよい。これをテイラー展開と呼ぶ。

\begin{eqnarray}
f(x)&=&f(a)+f'(a)(x-a)+\frac{1}{2!} f''(a)(x-a)^2+\frac{1}{3!}f'''(a)(x-a)^3+\cdots\\
&=& \sum_{k=0}^{\infty}\frac{f^{(k)}(a)}{k!}(x-a)^k
\end{eqnarray}

以前導いた等躍度運動の式を用いて、テイラー展開の性質3つが成り立つ理由を説明する。

1. 色々な関数をの無限べき級数で表してもよい。
2. 項の係数はである。
3. べき級数は低次の項だけ計算すれば大体合っている。

等躍度運動の式の変形

 説明のため、3次のべき級数である等躍度運動の式を再掲する。

\begin{eqnarray}
f(t)=\frac{1}{6}j t^3+\frac{1}{2}a_0t^2+v_0t+x_0
\end{eqnarray}

昇べきの順に並びかえる。

\begin{eqnarray}
f(t)=x_0+v_0t+\frac{1}{2}a_0t^2+\frac{1}{6}j t^3
\end{eqnarray}

係数を階乗で表す。

\begin{eqnarray}
f(t)=\frac{1}{0!}x_0+\frac{1}{1!}v_0t+\frac{1}{2!}a_0t^2+\frac{1}{3!}j t^3
\end{eqnarray}

今まではでと考えていたが、においてと考えて式を書き直す。

\begin{eqnarray}
f(t)&=&\frac{1}{0!}x_0+\frac{1}{1!}v_0(t-a)+\frac{1}{2!}a_0(t-a)^2+\frac{1}{3!}j (t-a)^3\\
&=&\sum_{k=0}^{3}\frac{C_n}{k!}(t-a)^k
\end{eqnarray}

次数が無限でないことを除けば、等躍度運動の式とテイラー展開の式はとても良く似ていることが分かる。 

1. なぜ色々な関数をのべき級数で表していいのか

仮想的にテイラー展開でもを時間、を位置と考えてみると、一階微分は速度、二回微分は加速度、三回微分は躍度…に相当する。速度(一階微分)や加速度(二階微分)が最終位置(元の関数)にどのように影響するかを、物体の運動と同じように適用することで、色々な関数を近似できる。

「対象の関数はべき級数とは限らないのにそうしていいのか？」という疑問が残るが、テイラー展開には「無限回微分可能」かつ「が基準点から近い」という縛りがあるので、べき級数でなくとも初速度や初加速度からの影響は「自然な」(が1つの値に定まる)影響しか受けない、と言えるのである。（もし成り立たないとすればとが収束半径よりも離れているということ）

テイラー展開の手順を図字する。

ある関数において、をのべき級数で表したい。まずテイラー展開の基準点を決定する。

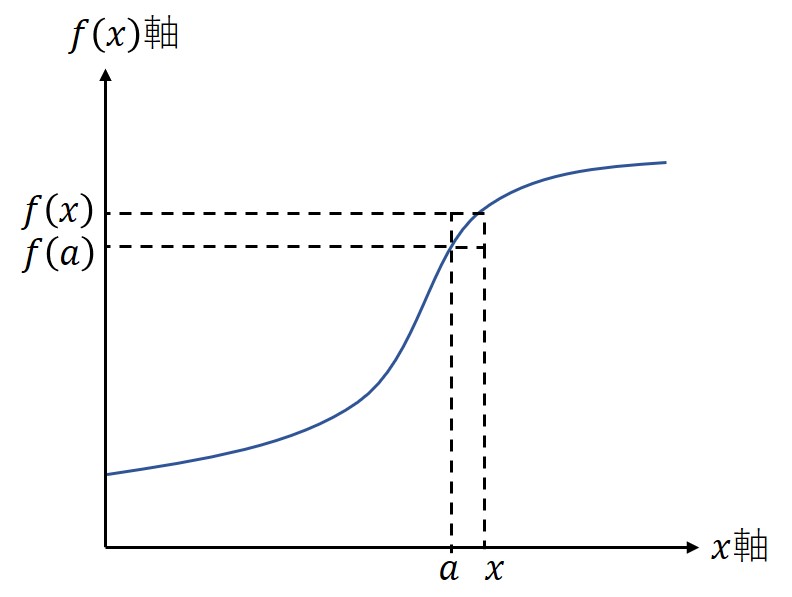
分かりやすいように目標地点を拡大する。とが近いという前提があるのでだけで近似してもそれなりに近い値になる。これは位置項だけによる近似と等価である。

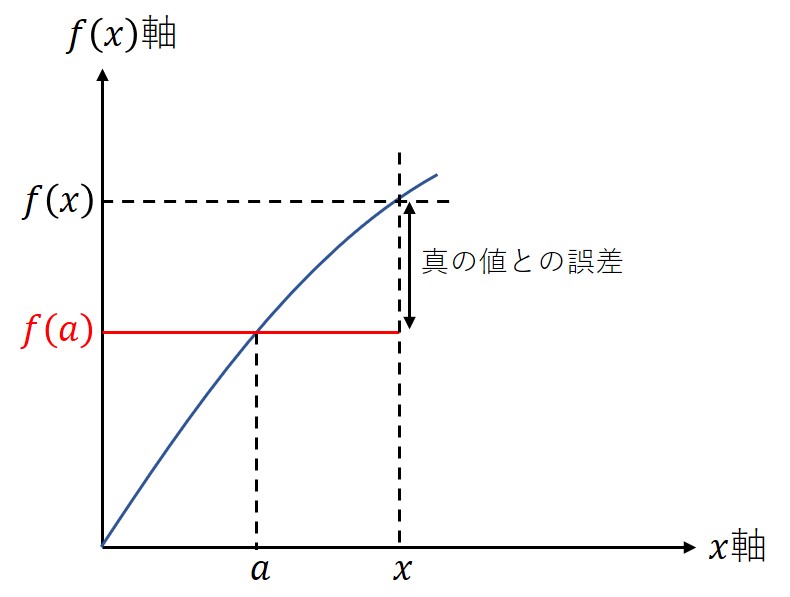
ここからがテイラー展開である。点における傾きに底辺長を掛けて先ほどのに加える。これは速度項による補正と等価であり、この処理で誤差がグッと小さくなることが分かる。テイラー展開のべき級数がの形になっているのは、この底辺長に対応していることによる。

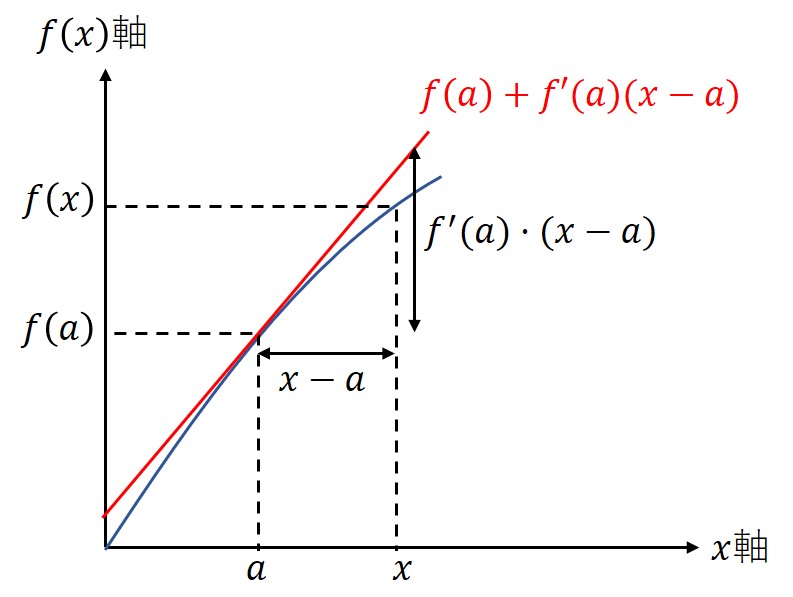
さらに加速度項による近似を加える。この時の係数は視覚的に明らかではないので後述する。

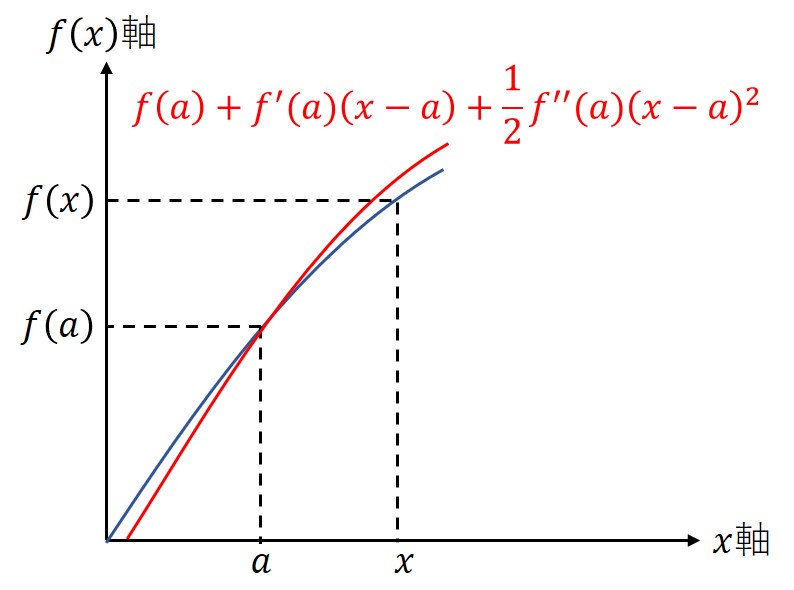
位置、速度、加速度と反映するごとに、だんだん誤差が小さくなっていることが分かる。

 2. なぜ項の係数はなのか

これについては先ほどの章でほぼ答えが出ている。等躍度運動の式を見れば、加速度項から距離を生むための係数は、躍度項から速度を生むための項はであった。このという係数は、回微分した項から距離を生むための係数に等しいのである。

3. なぜ途中まで計算すれば大体合っているのか

の強さ

等躍度運動の位置の式を再掲する。簡単のため、運動開始の時刻はとした。

\begin{eqnarray}
f(t)=\frac{1}{0!}x_0+\frac{1}{1!}v_0t+\frac{1}{2!}a_0t^2+\frac{1}{3!}j t^3
\end{eqnarray}

を代入してして位置を計算する。

\begin{eqnarray}
x &=& x_0+10v_0+ \frac{100}{2}a_0+\frac{1000}{6}j
\end{eqnarray}

係数にもよるが、がとても強いことが分かる。時間が経過するにつれて、位置の値はほとんど躍度項が占めることになる。

ここで逆にがとても小さい場合を考える。を代入して計算する。

\begin{eqnarray}
f(t)&=& x_0+ 0.1v_0+\frac{0.01}{2}a_0+\frac{0.001}{6}j
\end{eqnarray}

小さい時間においては、躍度項や加速度項はとても小さくなってしまい、速度項まで計算すれば大体の近似が可能になる。これがテイラー展開の本質の一つである。

項を拡張して無限のベキ関数を考える。これは躍度の時間変化率、そのまた時間変化率、と無限に考えていくことに等しい。は数列であり、項の比例係数が格納されている。

\begin{eqnarray}
x &=& x_0+v_0t+ \frac{1}{2}a_0t^2+\frac{1}{6}j t^3 +\cdots\\
&=& \frac{1}{0!}x_0+\frac{1}{1!}v_0t+ \frac{1}{2!}a_0t^2+\frac{1}{3!}j t^3 +\cdots\\
&=& \sum_{k=0}^{\infty} \frac{C_k}{k!}t^k
\end{eqnarray}

等躍度運動の場合、という訳である。

等躍度運動

等加速度運動

以前、空気抵抗を無視した自由落下運動、すなわち等加速度運動について書いた。

例えば宇宙空間でロケットを操縦しているとき、フットペダルを一定量踏めば、ブースターが一定の推力を発揮し、ロケットはすなわちの加速度で等加速度運動するだろう。

等躍度運動

しかし、実際にはフットペダルをいきなり一定量踏むのではなく、徐々に踏み込んでいくことになる。その間、推力は増加していくので加速度も一定にはならず、やはり一定の変化率で増加していく。

加速度が一定の割合で時間変化していく様子を微分方程式で表す。この比例定数、すなわち加速度の時間変化率を躍度(jerk)と言い、と書く。

\begin{equation}
\dot{a}=j
\end{equation}

両辺を時間で積分していくと、速度や位置を求めることができる

加速度を求める。

\begin{eqnarray}
\int \dot{a} dt&=&\int j dt\\
a &=& j t+C_1 \tag{1}
\end{eqnarray}

速度を求める。

\begin{eqnarray}
\int a dt&=&\int (j t+C_1) dt\\
v &=& \frac{1}{2}j t^2+C_1t+C_2 \tag{2}
\end{eqnarray}

位置を求める。

\begin{eqnarray}
\int v dt&=&\int \frac{1}{2}j t^2+C_1t+C_2 dt\\
x &=& \frac{1}{6}j t^3+\frac{1}{2}C_1t^2+C_2t+C_3 \tag{3}
\end{eqnarray}

微分方程式を解いて位置が求められた。

式の分析

式(1), (2), (3)にそれぞれを代入することにより、任意定数、、がそれぞれの時の, , を表すことが分かる。分かりやすいように、、と書き直す。

\begin{eqnarray}
x &=& \underline{\frac{1}{6}j t^3}+ \underline{\frac{1}{2}a_0t^2+v_0t+x_0}
\end{eqnarray}

右辺第2項から第4項は等加速度運動と全く同じで、新たにを加えた形になっている。これは等速運動と等加速度運動の関係と同様である。

これは積分のたびに、係数がの指数で割られ、分母にという積が出来ているためである。すなわちを意味する。

\begin{eqnarray}
x &=& \frac{1}{3!}j t^3+ \frac{1}{2!}a_0t^2+\frac{1}{1!}v_0t+\frac{1}{0!}x_0\\
&=&\sum_{k=0}^3 \frac{C_k}{k!}t^k
\end{eqnarray}

項の比例定数を数列で表すと、等躍度運動の位置の式はこのように短く書ける。この時記号の便宜的に、先ほどまでとはの次数対応が変わっていることに注意。

三平方の定理の証明

三平方の定理(ピタゴラスの定理)を証明する。

すなわち、上図のような直角三角形を考えたとき、

\begin{equation}
a^2+b^2=c^2
\end{equation}

が成り立つことを示す。

証明

 合同な直角三角形を下図のように4つ配置した場合を考える。

ここで大きな四角形は、明らかに四辺の長さがの正方形である。

また白い小さな四角形は、四辺の長さが、四隅の角が垂直でない2角の和 であるので、やはり正方形である。

「大きな正方形の面積」は、「小さな正方形の面積と直角三角形4つの面積の和」に等しいので、以下の等式が成り立つ。

\begin{eqnarray}
(a+b)^2=c^2+4\frac{a\cdot b}{2}
\end{eqnarray}

両辺を整理していく。

\begin{eqnarray} \require{cancel}
a^2+2ab+b^2&=&c^2+2ab\\
a^2+\cancel{2ab}+b^2&=&c^2+\cancel{2ab}\\
a^2+b^2&=&c^2
\end{eqnarray}

両辺のがちょうど打ち消し合い、三平方の定理が導かれた。

自由落下運動 - 空気抵抗有無の比較2

特殊解(再掲)

前回計算した速度と位置の特殊解(で)を再度書く。

ここでは落下物の速度、は位置、は重力加速度、は時間、は空気抵抗係数、は落下物の質量、は任意定数である。いずれも上方向(重力と逆方向)をとしていることに注意。

空気抵抗なし

速度

\begin{eqnarray}
v=-gt
\end{eqnarray}

位置

\begin{eqnarray}
x=-\frac{1}{2}gt^2
\end{eqnarray}

空気抵抗あり

速度

\begin{eqnarray}
v&=&\frac{mg}{k} \left[ \exp{\left(-\frac{kt}{m}\right)}-1 \right]\\
\end{eqnarray}

位置

\begin{eqnarray}
x=-\frac{m^2g}{k^2} \exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k}t+\frac{m^2g}{k^2}
\end{eqnarray}

定数の代入

以前、スカイダイビングの到達速度を基に、空気抵抗係数の計算を行った。その値をそのまま使用して落下速度と位置をプロットする。すなわち、、とする。

空気抵抗なし

速度

\begin{eqnarray}
v=-10t
\end{eqnarray}

位置

\begin{eqnarray}
x&=&-\frac{1}{2} \cdot 10t^2\\
&=&\underline{-5t^2}
\end{eqnarray}

空気抵抗あり

速度

\begin{eqnarray}
v&=&\frac{mg}{k} \left[ \exp{\left(-\frac{kt}{m}\right)}-1 \right]\\
&=&\frac{60 \cdot 10}{12} \left[ \exp{\left(-\frac{12t}{60}\right)}-1 \right]\\
&=&\underline{50 \left[ \exp{\left(-0.2t\right)}-1 \right]}
\end{eqnarray}

位置

\begin{eqnarray}
x&=&-\frac{m^2g}{k^2} \exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k}t+\frac{m^2g}{k^2}\\
&=&-\frac{60^2 \cdot 10}{12^2} \exp{\left(-\frac{12t}{60}\right)}-\frac{60 \cdot 10}{12}t+\frac{60^2 \cdot 10}{12^2}\\
&=&-250 \exp{(-0.2t)}-50t+250
\end{eqnarray}

プロット

これで準備が整い、とをの関数としてプロットすることができる。

落下速度のグラフ

落下位置のグラフ

導かれた式の形は全く違うが、確かにオレンジのグラフは空気抵抗のある落下運動になっていることが分かる。速度は、青のグラフで表した空気抵抗なしから徐々に遅れ始め、最終的には一定速度で安定する。

落下位置も最初は空気抵抗なしとほぼ同じであるが、だんだん空気抵抗の効きが大きくなり、最終的には等速運動になっていることが分かる。

このように、物体にかかる力だけから出発して、速度や位置などの情報を正確に導けることが微分方程式の面白さである。

自由落下運動 - 空気抵抗有無の比較1

これまでに導いた空気抵抗無しと有りの2つの自由落下運動を比較してみよう。導いた一般解を再度書き出す。

ここでは落下物の速度、は位置、は重力加速度、は時間、は空気抵抗係数、は落下物の質量、は任意定数である。いずれも上方向(重力と逆方向)をとしていることに注意。

空気抵抗なしの自由落下

一般解

前回求めた一般解を再掲する。

速度

\begin{eqnarray}
v=-gt+v_0 \tag{1}
\end{eqnarray}

位置

\begin{eqnarray}
x=-\frac{1}{2}gt^2+v_0t+x_0 \tag{2}
\end{eqnarray}

特殊解

初期値を代入して特殊解を作る。

今回はにおいて、基準点から静かに落下させたとする。すなわち初期値はでになる。

空気抵抗なしの場合、式(1)より、式(2)よりである。

速度

\begin{eqnarray}
v=-gt
\end{eqnarray}

位置

\begin{eqnarray}
x=-\frac{1}{2}gt^2
\end{eqnarray}

空気抵抗ありの自由落下

一般解

前回求めた一般解を再掲する。

速度

\begin{equation}
v=C_1\exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k} \tag{3}
\end{equation}

位置

\begin{eqnarray}
x&=&-\frac{mC_1}{k}\exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k}t+C_2 \tag{4}
\end{eqnarray}

特殊解

同様に、初期値をでとして任意定数を定める。

任意定数の計算

式(3)にを代入して、

\begin{eqnarray}
v&=&C_1\exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k} \tag{3}\\
0&=&C_1\exp(0)-\frac{mg}{k}\\
C_1&=&\frac{mg}{k}
\end{eqnarray}

式(4)にを代入して、

\begin{eqnarray}
x&=&-\frac{mC_1}{k}\exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k}t+C_2 \tag{4}\\
0&=&-\frac{m}{k}\frac{mg}{k}\exp(0)-0+C_2\\
C_2&=&\frac{m^2g}{k^2}
\end{eqnarray}

これらの定数を一般解に代入すると特殊解になる。

速度

\begin{eqnarray}
v&=&\frac{mg}{k} \exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k}\\
&=&\frac{mg}{k} \left[ \exp{\left(-\frac{kt}{m}\right)}-1 \right]
\end{eqnarray}

位置

\begin{eqnarray}
x&=&-\frac{m}{k} \frac{mg}{k} \exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k}t+\frac{m^2g}{k^2}\\
&=&-\frac{m^2g}{k^2} \exp{\left(-\frac{kt}{m}\right)}-\frac{mg}{k}t+\frac{m^2g}{k^2}
\end{eqnarray}

何が言いたいか

同じような微分方程式から生み出されたにもかかわらず、導かれた速度や位置の式は空気抵抗の有無で大きく異なっている。次回これらの運動をグラフにプロットし、本当に似た運動を示しているのか確かめる。