2020-02-23

C14年代測定を式で表す

概要

土中から発掘された遺跡や化石が何年前のものなのか分析するための手法、 $\rm C14$ 年代測定を式で示す。

原理

炭素の放射性同位体 $\rm C14$ は宇宙線により毎年生産され、同時にβ崩壊により毎年消滅している。これらの平衡により地球上の炭素原子に占める $\rm C14$ の割合は $\displaystyle \frac{1}{10^{12}}$ に保たれている。

また、生物は常に環境からの炭素摂取と排出を繰り返しているため、体内の $\rm C14$ もまた同じ割合に保たれている。しかし生物が死亡すると炭素の摂取が止まるため、遺骸内の $\rm C14$ 量は減少していく。

これを用いて生物がいつ死亡したかを判定するのが $\rm C14$ 年代測定である。どのように年代を分析するかを式で表す。

$\rm C14$ の半減期は5730年であり、5730年経過するごとに遺骸内の $\rm C14$ は元の量の半分になる。これは以下のような式で表せる。

\begin{eqnarray}
x \times \left( \frac{1}{2} \right) ^\frac{y}{5730} = z
\end{eqnarray}

ここで $x$ は当初の $\rm C14$ の割合、 $y$ が経過した年数、 $z$ が経過後の $\rm C14$ の割合である。

$x$ に死んだ直後における $\rm C14$ の割合 $\displaystyle \frac{1}{10^{12}}$ 、 $z$ に現在の(測定された) $\rm C14$ の割合を代入して $y$ を求めることができる。

$y$ について式変形していく。

\begin{eqnarray}
\left( \frac{1}{2} \right) ^\frac{y}{5730} &=& \frac{z}{x}\\
2 ^{\frac{-y}{5730}} &=& \frac{z}{x}\\
\end{eqnarray}

両辺の $\log_2$ を取る。

\begin{eqnarray}
{\frac{-y}{5730}} &=& \log_2 {\frac{z}{x}}\\
y&=&-5730 \log_2 {\frac{z}{x}}
\end{eqnarray}

$x = \frac{1}{10^{12}}$ を代入する。

\begin{eqnarray}
y&=&-5730 \log_2 {(10^{12}z)}
\end{eqnarray}

経過年数 $y$ を求める式が導かれた。変数は測定値 $z$ だけなので、 $\rm C14$ の割合を測定するだけで年代測定ができることがわかる。

この手法は化石などの生物遺骸には有効だが、土器などの非生物は測定出来ない。同時に出土した木材や食材を用いて間接的に測定する必要がある。

2020-02-15

バーゼル問題

概要

$s$ 次ゼータ関数 $\displaystyle \zeta(s)=\sum_{k=1}^{\infty}\frac{1}{k^s}$ の収束判定を行いたい。これまでに $\zeta(1)$ は無限大に発散し、 $\zeta(2)$ は2よりも小さい数に収束することを示してきた。

$\zeta(2)$ が実際いくつに収束するのかを求める。以下に $\zeta(2)$ を書き下しておく。

\begin{eqnarray} \zeta(2)&=&\sum_{k=1}^{\infty}\frac{1}{k^2}\ &=&\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\cdots \end{eqnarray}

導出

$\sin x$ のマクローリン展開を書き下す。

\begin{eqnarray} \sin x&=&x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-\frac{1}{7!}x^7+\cdots\ \end{eqnarray}

$x \neq 0$ として、両辺を $x$ で割る。

\begin{eqnarray} \frac{\sin x}{x}&=&1-\frac{1}{3!}x^2+\frac{1}{5!}x^4-\frac{1}{7!}x^6+\cdots \end{eqnarray}

右辺の無限べき関数を因数分解したい。どうすれば良いだろうか？

べき関数 $\displaystyle y = \sum_{n=0}^{\infty} {a_n} x^n$ が $x$ 軸と交差する点、 $\pm \pi, \pm 2\pi, \pm 3\pi, \cdots$ を用いて、右辺を因数分解できる。

\begin{eqnarray} \frac{\sin x}{x}&=&\left( 1-\frac{x}{\pi} \right) \left( 1+\frac{x}{\pi}\right) \left( 1-\frac{x}{2\pi}\right) \left( 1+\frac{x}{2\pi}\right)\left( 1-\frac{x}{3\pi}\right) \left( 1+\frac{x}{3\pi}\right)\cdots \end{eqnarray}

※ この時、右辺を定数倍したものも解を満たすが、 $\displaystyle \lim_{x \to 0} \frac{\sin {x}}{x}=1$ を用いて本式に定まる。

$(a+b)(a-b)=a^2-b^2$ を用いて右辺を変形する。 \begin{eqnarray} \frac{\sin x}{x}&=&\left( 1-\frac{x^2}{\pi^2}\right)\left( 1-\frac{x^2}{2^2\pi^2}\right)\left( 1-\frac{x^2}{3^2\pi^2}\right)\cdots\\ &=&1- \left( \frac{1}{\pi^2}+\frac{1}{2^2\pi^2} + \frac{1}{3^2\pi^2} \cdots \right) x^2 + \cdots \end{eqnarray} 展開して昇べきの順にまとめた。

マクローリン展開形式と昇べき形式の $x^2$ の項を比較する。これらは等しいはずなので以下が成り立つ。 \begin{eqnarray} \frac{1}{3!} &=& \frac{1}{\pi^2}+\frac{1}{2^2\pi^2} + \frac{1}{3^2\pi^2}+\cdots \\ \frac{1}{6} &=& \frac{1}{\pi^2} \left( \frac{1}{1^2}+\frac{1}{2^2} + \frac{1}{3^2} + \cdots \right)\\ \frac{\pi^2}{6} &=& \frac{1}{1^2}+\frac{1}{2^2} + \frac{1}{3^2} + \cdots \\ \end{eqnarray}

ここで右辺は $\zeta(2)$ の定義そのものであるので、以下のように表せる。 \begin{eqnarray} \displaystyle \zeta(2)=\sum_{k=1}^{\infty}\frac{1}{k^2}=\frac{\pi^2}{6} \\ \end{eqnarray}

また、 $\displaystyle \frac{\pi^2}{6}=1.64 \cdots$ であるので、 $\zeta(2)$ は2よりも小さい数に収束することが確かめられた。

2020-01-12

マクスウェル方程式を導く準備

マクスウェル方程式とは

電磁気に関する実験的事実をスタートとして、論理的考察(電場と磁場)を加え、微分方程式で表したもの。

4つの実験的事実が4つの方程式で表される。マクスウェル方程式を解くことで、電磁波の存在や、光もまた電磁波であることなどの重要な事実が導かれる。

実験的事実

マクスウェル以前に実験で確かめられた4つの法則。

1. 電荷のクーロンの法則

電荷には+と-の2種類が存在する
電荷が同じ符号だと斥力、違う符号だと引力を持つ
引力と斥力はどちらも、電荷の量に比例し、距離の2乗に反比例する

2. 電磁誘導の法則

電線に磁石を近づけたり遠ざけたりすると電線の両端に電位差が発生する
発生する電位差は、磁石を動かす速度に比例する
発生する電位差の向きは、アンペールの法則で磁力の変動を妨げる方向になる

3. 磁荷のクーロンの法則

磁荷にはN(+)とS(-)の2種類が存在する
磁荷が同じ符号だと斥力、違う符号だと引力を持つ
引力と斥力はどちらも、磁荷の量に比例し、距離の2乗に反比例する
単磁極は存在せず、磁石は必ずN極とS局のペアで存在する

4. アンペールの法則

電線に電流を流すと、周囲に磁力が発生する
磁力の強さは、電流に比例し、電線からの距離に反比例する。
発生する磁力の向きは右ねじの法則にしたがう

論理的考察

実験的事実を解釈する際に想像されたもの。

電場

電荷に対して力を及ぼす空間のこと
電荷や電圧によって発生する

磁場

磁荷に対して力を及ぼす空間のこと
磁荷や電流によって発生する

電場と磁場の実在性

電場と磁場が「計算上便利だから導入された想像上の物なのか？それとも本当に存在するものなのか？」は電磁気学にとって重要な問題である。マクスウェル方程式を解くことにより、電場と磁場の実在が確かめられる。

マクスウェル方程式の二つの記法

マクスウェル方程式には「積分形」と「微分形」の2つの記法があり、「微分形」の方が有名。

積分形までは上記事実と論理的考察のみでたどり着くことができるが、微分形は積分形に対して純粋に数学的な書き換えを行わなければ得られない。

2019-08-18

一次元の熱方程式を導く

概要

十分細く、一次元とみなせる針金の温度分布と、その経時変化を考えたい。まず解くべき微分方程式を導出する。

針金上の座標を $x \: \rm{[m}]$ 、時間を $t \: \rm{[sec]}$ 、温度を $T(x,t) \: \rm{[K]}$ とする。

f:id:dai-ig:20190901110610j:plain:w480

また、熱の流れ $\Gamma (x,t) \: \rm{[J/sec]}$ を考える。

導出

熱の流れについての式

熱の流れ $\Gamma$ は温度の勾配 $\displaystyle \frac{\partial T}{ \partial x}$ に比例する。(フーリエの法則)

この関係は以下のように式で表せる。

\begin{equation} \Gamma (x,t)=-k\frac{\partial}{ \partial x} T(x,t) \tag{1} \end{equation}

ここで、温度 $T$ は $x$ と $t$ 両方の関数としたので、偏微分になる。

$k$ は熱流の通りやすさを示す、熱伝導率と呼ばれる正の比例定数であり、針金の材質で決まる。熱は温度が高い方から低い方に流れるので、温度勾配とは逆方向に流れる。そのため $k$ の前にマイナスがついている。

針金上の一次元区間 $(a, b )$ を考える。

f:id:dai-ig:20190901110810j:plain:w480

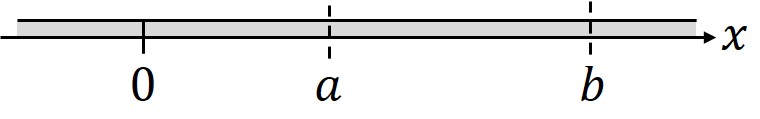
それぞれの点の熱流を式(1)形式で表す。

\begin{equation} \Gamma (a,t)=-k \left. \frac{\partial}{ \partial x} T(x,t)\right|_{x=a} \end{equation}

\begin{equation} \Gamma (b,t)=-k \left. \frac{\partial}{ \partial x} T(x,t)\right|_{x=b} \end{equation}

点 $a$ と点 $b$ を通した熱流の出入りの総和は以下のように書ける。

\begin{equation} \Gamma(b,t)-\Gamma(a,t)=\int^b_a \frac{\partial}{\partial x} \Gamma(x,t) dx \tag{2} \end{equation}

式(2)を確認するため、右辺の定積分を実際にやってみよう。

\begin{eqnarray} 右辺&=&\int^b_a \frac{\partial}{\partial x} \Gamma(x,t) dx \\ &=&\bigl[\Gamma(x,t) \bigr]^b_a \\ &=&\Gamma(b,t)-\Gamma(a,t) \\ &=& 左辺 \end{eqnarray}

等式が確認された。

式2に $\Gamma(a,t),\Gamma(b,t)$ および $\Gamma(x,T)$ の中身を代入する。

\begin{eqnarray} −k\frac{∂}{∂x}T(x,t)|_{x=a}+k\frac{∂}{∂x}T(x,t)|_{x=b}=−k\int^b_a\frac{∂^2}{∂x^2}Γ(x,t)dx \end{eqnarray}

熱量についての式

一方、区間 $(a,b)$ に蓄えられている熱量は以下のように書ける。

\begin{equation} Q(t)=c\int ^b_a T(x,t) dx \end{equation}

$c$ は物質の温まりにくさを示す正の比例定数であり、(単位長さ当たりの)熱容量と呼ばれる。値は針金の材質で決まる。

$Q(t)$ の時間変化を考える。両辺を $t$ で微分する。ここで、 $Q(t)$ は $t$ だけの関数なので全微分である。

\begin{eqnarray} \frac{d}{dt}Q(t)&=&c\frac{∂}{∂t}∫_a^b T(x,t) dx \\ &=& c∫_a^b \frac{∂}{∂t} T(x,t) dx \end{eqnarray}

微分と積分の順序を交換した。

二つの式を合体

熱量の保存則より以下の関係が成り立つ。

\begin{eqnarray} \frac{d}{dt} Q(t)=出入りする熱量の合計 \end{eqnarray}

左辺と右辺の中身はここまでに解っているので、それぞれ代入する。 \begin{eqnarray} c∫_a^b\frac{∂}{∂t} T(x,t) dx = k∫^b_a\frac{∂^2}{∂x^2} Γ(x,t) dx \end{eqnarray}

この関係が全ての $(a,b)$ で成り立つためには積分の対象が等しい必要がある。 \begin{eqnarray} c\frac{∂}{∂t}T(x,t)=k\frac{∂^2}{∂x^2}Γ(x,t) \end{eqnarray}

一次元の熱方程式が導かれた。この微分方程式を解くことで、針金の温度分布とその時間変化が求められる。

2019-05-28

円の面積の導出

幾何数学

概要

以前、弧の長さを用いて導出した等式、 $\displaystyle \lim_{x \to 0} \frac{\sin x}{x}=1$ を用いて、半径 $r$ を持つ円の面積を導出する。

導出

半径 $r$ の円に内接する正 $n$ 角形と円に外接する正 $n$ 角形を考える。 $n=6$ の場合を図に示す。

f:id:dai-ig:20200126145130p:plain:w480

下図のように、円と正 $n$ 角形をを $2n$ 等分して考える。

f:id:dai-ig:20200126145212p:plain:w480

まず二つの直角三角形と切り取られる扇形の面積を、円の半径 $r$ と中心角 $x$ を用いて表す。

小さな直角三角形の面積 $S_1$

斜辺が $r$ と定まることから底辺と高さを導ける。

f:id:dai-ig:20200126151223p:plain:w400

\begin{eqnarray} S_1&=&\frac{1}{2}\times r \cos x \times r \sin x\newline &=&\frac{r^2 \sin x \cos x}{2} \end{eqnarray}

切り取られる扇形の面積 $S_2$

未知の値。この値を求めてから $2n$ 倍すれば円の面積が求められる。

f:id:dai-ig:20200126151545p:plain:w360

大きな直角三角形の面積 $S_3$

底辺が $r$ と定まることから斜辺、高さの順に導ける。

f:id:dai-ig:20200126152030p:plain:w480

\begin{eqnarray} S_3&=&\frac{1}{2} \times r \times \frac{r \sin x}{\cos x}\ &=&\frac{r^2 \sin x}{2\cos x} \end{eqnarray}

面積の比較

図を重ねて比較すると明らかに以下の関係が成り立つ。

\begin{eqnarray} S_1<S_2<S_3 \end{eqnarray}

$S_1$ と $S_3$ に計算した値を代入する。

\begin{eqnarray} \frac{r^2 \sin x \cos x}{2}<S_2<\frac{r^2 \sin x}{2\cos x} \end{eqnarray}

$x > 0$ として全体を $x$ で割り、 $\displaystyle \frac{ \sin x }{ x }$ の形を作る。

\begin{eqnarray} \frac{ r^2 }{ 2 } \frac{ \sin x }{ x } \cos x&<&\frac{S_2}{x}&<&\frac{r^2}{2 }\frac{ 1 }{ \cos x }\frac{ \sin x}{ x } \end{eqnarray}

ここで、 $n$ 角形を、 $\infty$ 角形に近づけていく。この時中心角 $x$ は限りなく $0$ に近づく。

\begin{eqnarray} \lim_{x \to 0} \frac{ r^2 }{ 2 } \frac{ \sin x }{ x } \cos x&<& \lim_{x \to 0}\frac{S_2}{x}&<& \lim_{x \to 0}\frac{r^2}{2 }\frac{ 1 }{ \cos x }\frac{ \sin x}{ x } \end{eqnarray}

$\displaystyle \lim_{x \to 0}\frac{ \sin x }{x }=1$ を用いる。

\begin{eqnarray} \require{cancel} \lim_{x \to 0} \frac{ r^2 }{ 2 } \cancel {\frac{ \sin x }{ x } }\cos x&<& \lim_{x \to 0}\frac{S_2}{x}&<& \lim_{x \to 0}\frac{r^2}{2 }\frac{ 1 }{ \cos x }\cancel{\frac{ \sin x}{ x }} \newline \lim_{x \to 0}\frac{ r^2 }{ 2 }\cos x&<& \lim_{x \to 0}\frac{S_2}{x}&<& \lim_{x \to 0} \frac{ r^2 }{ 2 }\frac{1}{\cos x} \newline \frac{ r^2 }{ 2 }&<& \lim_{x \to 0}\frac{S_2}{x}&<& \frac{ r^2 }{ 2 } \end{eqnarray}

はさみうちの原理により、以下の関係が求められた。 \begin{eqnarray} \lim_{x \to 0}\frac{S_2}{x} = \frac{ r^2 }{ 2 } \end{eqnarray}

切り取る中心角 $x$ は一周分の中心角 $2 \pi$ を $2n$ 等分した角度なので、 $\displaystyle x=\frac{ 2 \pi }{ 2 n }=\frac{\pi }{ n }$ を代入する。

\begin{eqnarray} \lim_{n \to \infty}\frac{S_2}{\frac{ \pi }{ n }} &=& \frac{ r^2 }{ 2 } \newline \lim_{n \to \infty}\frac{nS_2}{\pi } &=&\frac{ r^2 }{ 2 } \end{eqnarray}

両辺を $2\pi$ 倍する。

\begin{eqnarray} \lim_{n \to \infty}2nS_2&=&\pi r^2 \end{eqnarray}

ここで左辺は、円を $2n$ 等分した扇型の $S_2$ を、再度 $2n$ 倍したものなので、元の円の面積に等しい。半径 $r$ を持つ円の面積が $\pi r^2$ で表されることが導かれた。

2019-05-13

x が0に近い時のsin x の性質弧の長さを用いる方法

数学幾何微分

循環論法

以前、扇型の面積を挟み打ちして $\displaystyle \lim_{x \to 0}\frac{\sin x}{x} =1$ を導出した。この手法は分かりやすいが、実は循環論法の問題がある。

半径 $r$ を持つ円の面積が $\pi r^2$ であることは定義されたことや自明なことではない。証明するには三角関数の積分が必要であり、その際に既に $\displaystyle \lim_{x \to 0}\frac{\sin x}{x} =1$ を知っている必要があるためである。

対策

円周率 $\pi$ の定義は円の直径 $2r$ と円周長の比であるので、半径 $r$ を持つ円の円周長が $2\pi r$ なことは定義されたこととして使用しても良い。これを出発点として $\displaystyle \frac{\sin x}{x} =1$ を導出すれば循環論法を回避できる。

導出

正 $n$ 角形

半径 $r$ の円に内接する正 $n$ 角形と外接する正 $n$ 角形を考える。下図に $n = 6$ の場合を示した。

f:id:dai-ig:20200126145130p:plain:w480

ここで、内接する正 $n$ 角形、円、外接する正 $n$ 角形の外周の長さをそれぞれ $A$ 、 $B$ 、 $C$ とする。これらの大小関係を比較すると、明らかに以下の関係が成り立つ。

\begin{eqnarray} A \lt B \lt C \end{eqnarray}

下図で色をつけた3本の線の長さに注目する。

f:id:dai-ig:20200209202950p:plain:w480

これらはそれぞれ $A$ 、 $B$ 、 $C$ を $2n$ で割ったものなので、大小関係は維持される。 \begin{eqnarray} \frac{ A }{2n }< \frac{ B }{ 2n } < \frac{ C }{ 2n } \end{eqnarray}

これらの3本の線の長さをを別の形式で表す。これらが直角三角形の高さまたは弧の長さであることを用いて線の長さを求める。

小さい直角三角形

f:id:dai-ig:20200209204018p:plain:w400

斜辺が $r$ と中心角 $x$ から高さが求まる。 \begin{equation} \frac{ A }{ 2n }=r \sin x \end{equation}

切り取られる円弧

f:id:dai-ig:20200209204059p:plain:w360

全体の円周 $2\pi r$ に角度の割合 $\frac{ x }{ 2\pi }$ を掛けた $rx$ が弧の長さになる。

\begin{equation} \frac{ B }{ 2n }=rx \end{equation}

大きい直角三角形

f:id:dai-ig:20200209204121p:plain:w480

今度は底辺が $r$ なので、まず斜辺 $\displaystyle \frac{ r }{ \cos x }$ 、次に高さ $\displaystyle r\frac{ \sin x }{ \cos x }$ が導かれる。

\begin{equation} \frac{ C }{ 2n }=r \frac{ \sin x }{ \cos x } \end{equation}

これらの長さの極限

求めた線の長さを $\frac{ A }{ 2n }$ 、 $\frac{ B }{ 2n }$ 、 $\frac{ C }{ 2n }$ に代入する。

\begin{equation} r\sin x \lt rx \lt r\frac{ \sin x }{ \cos x } \end{equation}

共通する $r$ を打ち消す。

\begin{equation} \sin x \lt x \lt \frac{ \sin x }{ \cos x } \end{equation}

$x\neq 0$ として全体を $\sin x$ で割る。

\begin{equation} 1 < \frac{ x }{ \sin x } < \frac{ 1 }{ \cos x } \end{equation}

全体の逆数をとる。不等号は逆向きになる。 \begin{equation} 1 > \frac{ \sin x }{ x } > \cos x \end{equation}

正 $n$ 角形の対角線は $2\pi$ ラジアンを $n$ 等分するので、中心角 $x$ は、そのさらに半分で以下のように表せる。

\begin{equation} x=\frac{ 2\pi }{ 2n }=\frac{ \pi }{ n } \end{equation}

ここで、内接、外接する $n$ 角形を $\infty$ 角形に近づけていく。この時、中心角 $x$ は限りなく $0$ に近づいていく。

\begin{equation} \lim_{x \to 0} 1> \lim_{x \to 0}\frac{ \sin x }{ x } > \lim_{x \to 0}\cos x\\ 1> \lim_{x \to 0}\frac{ \sin x }{ x } >1 \end{equation}

挟み打ちの原理より $\displaystyle \lim_{x \to 0}\frac{ \sin x }{ x } =1$ が導かれた。

2019-04-28

Markdown記法の練習&メモ

はてなブログ

Markdownルールの概要

はてなブログではMarkdown記法が使用できる。HTMLコードの代わりに、特定のコマンド文字を使って文を簡単にマークアップする記法である。

コマンド文字自体はブログに表示されないが、直前にスラッシュ\をつけるとコマンド文字をそのまま表示できる。（コマンドの機能は失われる）

コマンド文字一覧

字	名称	主な効果
#	シャープ	見出し化
\	スラッシュ	コマンド文字の表示
`	バッククオート	コード表示
+	プラス	リスト化
*	アスタリスク	強調表示
_	アンダーバー	強調表示
>	右アングル	引用表示
-	ハイフン	水平線
^	ハット	上付き
\|	縦線	表作成

見出し1

# 見出し1

<h1>になる。ブログやエントリーのタイトルと同格。SEO的には良くないかもしれない。

見出し2

## 見出し2

#が多いほど小さな見出しになり、<h2>になる。記事内の見出しで一番強いのはこれぐらいか。

見出し3

### 見出し3

<h3>になる。サブセクションぐらい。

見出し4

#### 見出し4

<h4>レベルになる。サブサブセクションぐらい。

見出し5

##### 見出し5

<h5>になる。あまり使わなそう。

見出し6

###### 見出し6

<h6>になる。あまり使わなそう。

# 見出し7

####### 見出し7

<h6>になる。/#を増やして意味があるのは6個まで。

コード記法

## コード記法

`（バッククォート）で囲むとコードをそのまま表示できる。'ではないことに注意。

a
b
c
d

```で段落ごと囲むと段落ごとコード表示。

強調表示

*test

*単独では効果がない。文字列を囲んで使用する。

test
↑強調レベル1。*で囲む。

test
↑強調レベル2。**で囲む。

test
↑強調レベル3。***で囲む。

水平線

↑ハイフン3つ

↑ハイフン4つ

↑ハイフン5つ

ハイフン3個以上で分割線。効果は何個でも同じなので見やすいように書けばよい。

引用

テスト

> テスト

数式

[tex: y=ax²+bx+c]

[tex: y=ax^2+bx+c]

いつも通りに入力するとMarkdownが優先されてしまい、数式モードにならない。

$y=ax^2+bx+c$

[tex: y=ax\^2+bx+c]

\begin{eqnarray} y=ax^2+bx+c \end{eqnarray}

\begin{eqnarray}
y=ax\^2+bx+c
\end{eqnarray}

^などを\バックスラッシュでエスケープするとMathjaxを使用可能だがなかなか面倒。

コマンド文字以外のルール

編集時の改行は反映されない。半角スペース2つ入力で改行される。（わかりにくい）

2回改行して空行を作ると段落分けされる。

空行を2行以上空けても段落は1回だけしか分かれない。

画像について

f:id:dai-ig:20190428164734j:plain

[f:id:dai-ig:20190428164734j:plain]

f:id:dai-ig:20190428164734j:plain:w200

[f:id:dai-ig:20190428164734j:plain:w200]

画像タグ。はてなブログの機能で自動入力される。w200の部分で横幅を指定できる。

リンク

A4の宇宙

[A4の宇宙](https://a4.hateblo.jp)

概要

原理

概要

導出